Las cónicas (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:47 27 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:18 28 mar 2009 Coordinador (Discusión | contribuciones) (→Elipse) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| ==Las cónicas como lugares geométricos== | ==Las cónicas como lugares geométricos== | ||
| ===Elipse=== | ===Elipse=== | ||
| - | {{Caja_Amarilla|texto=Dados dos puntos F_1 y F_2 llamdos '''focos'''... | + | {{Caja_Amarilla|texto=Dados dos puntos <math>F_1\,</math> y <math>F_2\,</math> llamados '''focos''', y una distancia <math>k\,</math>, llamada ''constante de la elipse'' (<math>k > d(F_1,F_2)\,</math>), se llama '''elipse''' al lugar geométrico de los puntos <math>P\,</math> del plano cuya suma de distancias a los focos es igual a <math>k\,</math>: |
| + | |||
| + | {{Caja|contenido=<math>d(P,F_1)+d(P,F_2)=k</math>}} | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | ====Construcción de la elipse==== | ||
| + | {{AI2|titulo=Actividad interactiva: ''Potencia de un punto respecto a una circunferencia''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1:''' En la siguiente escena vamos a calcular la potencia del punto P(6,4) respecto de la circunferencia de centro O(0,0) y radio r=3. | ||
| + | |actividad=Calcula en tu cuaderno cuanto vale la potencia de ese punto respecto a la circunferencia y comprueba los resultados en la escena. | ||
| + | |||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/geogebra/elipse/elipse_construccion_1.html | ||
| + | width=520 | ||
| + | height=410 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/geogebra/elipse/elipse_construccion_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | Activa la traza, desliza el punto P y observa. | ||
| + | |||
| + | #¿Qué tipo de curva describe la traza de P? | ||
| + | #¿Qué representan los segmentos morados? | ||
| + | #¿Qué propiedad cumplen todos los puntos por los que pasa P? | ||
| + | #¿Qué ocurre si pones c=0? | ||
| + | |||
| + | }} | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 12:18 28 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
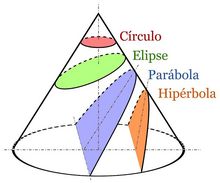
Secciones cónicas
Se denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. Según como corte el plano al cono tendremos (ver figura):
La primera definición de sección cónica aparece en Grecia, cerca del año 350, donde las definieron como secciones de un cono circular recto. Los nombres de hipérbola, parábola y elipse se deben a Apolonio de Pérgamo. |  |
Construcción de las cónicas
Las cónicas como lugares geométricos
Elipse
Dados dos puntos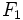 
y 
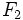llamados focos, y una distancia 
, llamada constante de la elipse (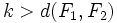
), se llama elipse al lugar geométrico de los puntos 
del plano cuya suma de distancias a los focos es igual a :
|
d(P,F1) + d(P,F2) = k |
Construcción de la elipse
 Actividad interactiva: Potencia de un punto respecto a una circunferencia
Actividad 1: En la siguiente escena vamos a calcular la potencia del punto P(6,4) respecto de la circunferencia de centro O(0,0) y radio r=3.
Actividad: Calcula en tu cuaderno cuanto vale la potencia de ese punto respecto a la circunferencia y comprueba los resultados en la escena.
Activa la traza, desliza el punto P y observa.
|
