Sucesos aleatorios (3ºESO)
De Wikipedia
| Revisión de 09:18 8 jun 2009 Coordinador (Discusión | contribuciones) (→Experimentos y sucesos aleatorios) ← Ir a diferencia anterior |
Revisión de 09:18 8 jun 2009 Coordinador (Discusión | contribuciones) (→Espacio muestral) Ir a siguiente diferencia → |
||
| Línea 36: | Línea 36: | ||
| }} | }} | ||
| <br/> | <br/> | ||
| - | {{ejercicio|titulo=Ejercicios:''Espacio muestral'' | + | {{ejercicio|titulo=Ejercicios: ''Espacio muestral'' |
| |cuerpo= | |cuerpo= | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
Revisión de 09:18 8 jun 2009
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Experimentos y sucesos aleatorios
Un fenómeno o experimento aleatorio es aquel en el que no se puede preveer con certeza el resultado que va tener lugar al observar el fenómeno o al realizar el experimento.
- Al lanzar una moneda al aire, no sabemos si va a salir cara o cruz. Por tanto, se trata de un experimento aleatorio en el que los posibles resultados son "salir cara" o "salir cruz".
- Si nos preguntamos si lloverá mañana, caben dos posibilidades: "si" o "no", y no sabemos con certeza que ocurrirá.
Espacio muestral
Espacio muestral es el conjunto formado por todos los resultados de un experimento o
fenómeno aleatorio. Lo denotamos con la letra 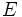 .
.
Ejemplo: Espacio muestral
- El espacio muestral asociado al lanzamiento de dos dados y anotar la suma de los puntos.
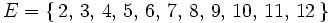
|
Ejercicios: Espacio muestral 1.Describe el espacio muestral asociado a cada uno de los siguientes experimentos aleatorios: a) Lanzar tres monedas. b) Lanzar tres dados y anotar la suma de los puntos obtenidos. c) Extracción de dos bolas de una urna que contiene cuatro bolas blancas y tres negras. d) El tiempo, con relación a la lluvia, que hará durante tres días consecutivos.Solución: a) Llamando C a obtener cara y X a la obtención de cruz, obtenemos el siguiente espacio muestral: E={(CCC),(CCX),(CXC),(XCC),(CXX),(XCX),(XXC),(XXX)} b) E={3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18} c) Llamando B a sacar bola blanca y N a sacar bola negra, tenemos: E={BB,BN,NN} d) Si llamamos L al día lluvioso y N al día sin lluvia, para tres días consecutivos se obtiene el siguiente espacio muestral: E={(LLL),(LLN),(LNL),(NLL),(LNN),(NLN),(NNL),(NNN)} |
Sucesos
Suceso de un fenómeno aleatorio es cada uno de los subconjuntos del espacio muestral E . Para designar cualquier suceso, tambien llamado suceso aleatorio, de un experimento aleatorio utilizaremos letras mayúsculas.
Al conjunto de todos los sucesos que ocurren en un experimento aleatorio se le llama espacio de sucesos y se designa por S .
Si E tiene un número finito, n, de elementos, el número de sucesos de E es 2n
Ejemplo: Sucesos
En el ejemplo anterior, determina los sucesos de E:
a)Salir múltiplo de 5. b)Salir número primo. c)Salir mayor o igual que 10.
a)Salir múltiplo de 5:
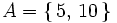
b)Salir número primo:
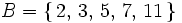
c)Salir mayor o igual que 10:
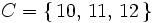
Analicemos los tipos mas frecuentes de sucesos.
Sucesos elementales son los que están formados por un solo resultado del
experimento.
Sucesos compuestos son los que estan formados por dos o más resultados del
experimento; es decir, por dos o más sucesos elementales.
Suceso seguro es el que se verifica al realizar el experimento aleatorio. Está
formado por todos los resultados posibles del experimento y, por tanto, coincide con el
espacio muestral.
Suceso imposible es el que nunca se verifica. Se representa por
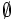 .
.

