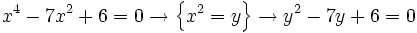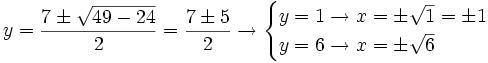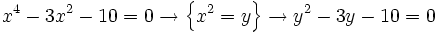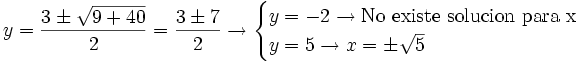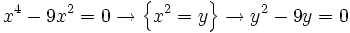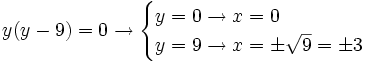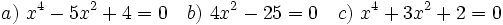Plantilla:Ecuaciones bicuadradas
De Wikipedia
| Revisión de 10:24 12 oct 2014 Coordinador (Discusión | contribuciones) (→Videotutoriales) ← Ir a diferencia anterior |
Revisión de 14:00 29 ago 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| {{Ejemplo|titulo=Ejemplo: ''Ecuaciones bicuadradas'' | {{Ejemplo|titulo=Ejemplo: ''Ecuaciones bicuadradas'' | ||
| - | |enunciado=Resuelve las ecuaciones: | + | |enunciado=:Resuelve las ecuaciones: |
| + | |||
| ::a) <math>x^4 - 7x^2 + 6 = 0\;\! </math> | ::a) <math>x^4 - 7x^2 + 6 = 0\;\! </math> | ||
| + | |||
| ::b) <math>x^4 - 3x^2 - 10 = 0\;\! </math> | ::b) <math>x^4 - 3x^2 - 10 = 0\;\! </math> | ||
| + | |||
| ::c) <math>x^4 - 9x^2 = 0 \;\! </math> | ::c) <math>x^4 - 9x^2 = 0 \;\! </math> | ||
| |sol= | |sol= | ||
| - | a) <math>x^4 - 7x^2 + 6 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-7y+6=0</math> | + | '''a)''' |
| + | :<math>x^4 - 7x^2 + 6 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-7y+6=0</math> | ||
| - | <math>y = \frac{7 \pm \sqrt{49-24}}{2}=\frac{7 \pm 5}{2} \rightarrow \begin{cases} y=1 \rightarrow x= \pm \sqrt 1 = \pm 1 \\ y=6 \rightarrow x= \pm \sqrt 6 \end{cases}</math> | + | :<math>y = \frac{7 \pm \sqrt{49-24}}{2}=\frac{7 \pm 5}{2} \rightarrow \begin{cases} y=1 \rightarrow x= \pm \sqrt 1 = \pm 1 \\ y=6 \rightarrow x= \pm \sqrt 6 \end{cases}</math> |
| - | '''Soluciones:''' <math>-1,\, 1,\, -\sqrt 6,\, \sqrt 6\,\!</math> | + | :'''Soluciones:''' <math>-1,\, 1,\, -\sqrt 6,\, \sqrt 6\,\!</math> |
| {{p}} | {{p}} | ||
| ---- | ---- | ||
| - | b) <math>x^4 - 3x^2 - 10 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-3y-10=0</math> | + | '''b)''' |
| + | :<math>x^4 - 3x^2 - 10 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-3y-10=0</math> | ||
| - | <math>y = \frac{3 \pm \sqrt{9+40}}{2}=\frac{3 \pm 7}{2} \rightarrow \begin{cases} y=-2 \rightarrow \mbox {No existe solucion para x} \\ y=5 \rightarrow x= \pm \sqrt 5 \end{cases}</math> | + | :<math>y = \frac{3 \pm \sqrt{9+40}}{2}=\frac{3 \pm 7}{2} \rightarrow \begin{cases} y=-2 \rightarrow \mbox {No existe solucion para x} \\ y=5 \rightarrow x= \pm \sqrt 5 \end{cases}</math> |
| - | '''Soluciones:''' <math> -\sqrt 5,\, \sqrt 5\,\!</math> | + | :'''Soluciones:''' <math> -\sqrt 5,\, \sqrt 5\,\!</math> |
| {{p}} | {{p}} | ||
| ---- | ---- | ||
| - | c) <math>x^4 - 9x^2 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-9y=0</math> | + | '''c)''' |
| + | :<math>x^4 - 9x^2 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-9y=0</math> | ||
| - | <math> y(y-9)=0 \rightarrow \begin{cases} y=0 \rightarrow x= 0 \\ y=9 \rightarrow x= \pm \sqrt 9 = \pm 3 \end{cases}</math> | + | :<math> y(y-9)=0 \rightarrow \begin{cases} y=0 \rightarrow x= 0 \\ y=9 \rightarrow x= \pm \sqrt 9 = \pm 3 \end{cases}</math> |
| - | '''Soluciones:''' <math>0,\, -3,\, 3\,\!</math> | + | :'''Soluciones:''' <math>0,\, -3,\, 3\,\!</math> |
| }} | }} | ||
| ===Videotutoriales=== | ===Videotutoriales=== | ||
Revisión de 14:00 29 ago 2016
Las ecuaciones bicuadradas Son ecuaciones de cuarto grado pero tienen una característica que las hace especiales: no tienen terminos de grado impar, es decir son de la forma
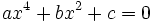
El truco para resolverlas es hacer el cambio de variable 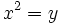 . Entonces, la ecuación quedará como una de segundo grado
. Entonces, la ecuación quedará como una de segundo grado
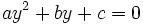
Una vez resuelta esta ecuación en  , tenemos que averiguar el valor de la
, tenemos que averiguar el valor de la  . Para ello desharemos el cambio de variable, haciendo
. Para ello desharemos el cambio de variable, haciendo 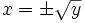 . En consecuencia, las soluciones
. En consecuencia, las soluciones 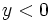 , las rechazaremos, ya que no darán solución para la
, las rechazaremos, ya que no darán solución para la 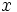 , quedándonos sólo con las soluciones de
, quedándonos sólo con las soluciones de 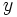 no negativas, cada una de las cuales dará dos soluciones para la
no negativas, cada una de las cuales dará dos soluciones para la 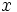 .
.
Ejemplo: Ecuaciones bicuadradas
- Resuelve las ecuaciones:
- a)
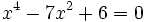
- a)
- b)
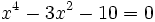
- b)
- c)
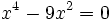
- c)
a)
- Soluciones:
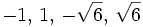
b)
- Soluciones:
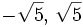
c)
- Soluciones:
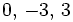
Videotutoriales
Videotutorial
Videotutorial
|
Actividad: Ecuaciones bicuadradas Resuelve las siguientes ecuaciones: Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|