Números naturales (3ºESO Aplicadas)
De Wikipedia
| Revisión de 07:03 6 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:19 6 sep 2016 Coordinador (Discusión | contribuciones) (→Descomposición de un número en factores primos) Ir a siguiente diferencia → |
||
| Línea 53: | Línea 53: | ||
| ==Descomposición de un número en factores primos== | ==Descomposición de un número en factores primos== | ||
| + | {{Descomposicion en factores}} | ||
| ==Mínimo común múltiplo== | ==Mínimo común múltiplo== | ||
Revisión de 07:19 6 sep 2016
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | Divisibilidad | WIRIS Geogebra |
(pág. 11-13)
Tabla de contenidos |
El conjunto de los números naturales
El conjunto de los números naturales es:
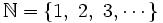
Se trata de un conjunto con infinitos elementos y sirven para:
- Contar (números cardinales: 1, 2, 3, ...).
- Ordenar (números ordinales: 1º, 2º, 3º, ...).
- Identificar y diferenciar los distintos elementos de un conjunto.
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en la prueba de cien metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
El conjunto de los números naturales: origen y definición.
El conjunto de los números naturales: origen y definición.
Tutorial de introducción al tema:
- Números naturales.
- Sistemas de numeración.
- Sistema de numeración decimal.
Hace unas horas tenía 16 años y el año que viene cumpliré 19. ¿Cómo explicas esta situación?
Ejercicios de autoevaluación sobre números naturales.
Existen dos teorías sobre el origen de la numeración, que además está relacionada con la cuestión de qué números aparecieron primero, los cardinales (1, 2, 3,...) o los ordinales (1º, 2º, 3º,...) La teoría que genera más consenso defiende el argumento de la necesidad. Todo habría comenzado a causa de la necesidad de contar objetos; por ello se habrían creado primero los números cardinales y después, los ordinales.
La otra teoría defiende la base espiritual de los números, que habrían tenido un uso ritual: cierto tipo de ceremonias requerían que los participantes se desplazaran o se situaran en un orden ritual preestablecido; por eso los números ordinales serían anteriores a los cardinales. Esta teoría además postula que los números se originaron en un lugar geográfico determinado, desde el que se propagaron al resto del mundo; también establece la división de los números naturales en pares e impares, considerando los impares masculinos y los pares, femeninos, una clasificación que comparten hoy en día muchas culturas del planeta.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 10)"
Véanse los artículos de la BBC:
- ¿Sabes que el 1 y el 2 no son del mismo género y que los números tienen personalidades?
- Lo que quizás no sabías de los números
Operaciones combinadas con números naturales
|
Ejercicios propuestos: Operaciones combinadas con números naturales |
Números primos y números compuestos
Propiedad
Conceptos de número primo y número compuesto. Tabla de números primos menores que 100. Conceptos de número primo y número compuesto. Conceptos de número primo y número compuesto. Breve explicación de qué son los números primos, cómo reconocerlos y cómo encontrarlos fácilmente Conceptos de número primo y número compuesto. Criba de Eratóstenes. Números primos. The building blocks of all natural numbers are the prime numbers. The early Greeks invented the system still used today for separating natural numbers into prime and composite numbers. (Disponibles los subtítulos en inglés) Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado) Determina cuáles de los siguientes números son primos, cuáles son compuestos, y cuáles no son ni primos ni compuestos: 24, 2, 1 y 17. |
- Actividad en la que puedes ver si un número es primo o compuesto.
- Actividad en la que debes separar los números primos de los compuestos.
Introducción a los números primos y compuestos.
Repaso sobre números primos y compuestos.
Actividad en la que aprenderás a determinar si un número es primo o compuesto.
Actividad en la que deberás decidir si un número es primo o compuesto.
Actividad en la que deberás decidir si un número es primo o compuesto.
Actividad en la que deberás pulsar sobre los números primos.
Identifica números primos.
Identifica números compuestos.
Test de 10 preguntas sobre números primos y compuestos.
Ejercicios de autoevaluación sobre números primos.
Ejercicios de autoevaluación sobre números compuestos.
Criterios de divisibilidad
Los siguientes criterios nos permiten averiguar si un número es divisible por otro de una forma sencilla, sin necesidad de realizar una división.
| Divisible por: | Criterio |
|---|---|
| 2 | El número acaba en 0 ó cifra par. |
| 3 | La suma de sus cifras es un múltiplo de 3. |
| 4 | El número formado por las dos últimas cifras es múltiplo de 4. |
| 5 | La última cifra es 0 ó 5. |
| 6 | El número es divisible por 2 y por 3. |
| 7 | La diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es 0 ó un múltiplo de 7. |
| 8 | El número formado por las tres últimas cifras es múltiplo de 8. |
| 9 | La suma de sus cifras es múltiplo de 9. |
| 10 | La última cifra es 0. |
| 11 | Se suman las cifras que forman el número de forma alternativa y se restan los resultados para ver si da un múltiplo de 11 (El cero también lo es) |
Los números que aparecen en verde se corresponden con aquellos cuyo criterio es un proceso que se puede usar de forma recursiva, es decir, si después de aplicarlo no sabemos si el número al que hemos llegado es múltiplo del número en cuestión, podemos aplicar nuevamente el criterio sobre ese resultado.
|
Ejercicios propuestos: Divisibilidad. Números primos y compuestos. |
Descomposición de un número en factores primos
Se le llama descomposición factorial o factorización de un número, a su expresión como producto de potencias de números primos.
Descomposición en factores primos
Cualquier número puede expresarse como producto de potencias de números primos.
El procedimiento es el siguiente:
- Lo dividimos por el menor número primo que podamos.
- El cociente que haya resultado lo colocamos debajo del número.
- Si podemos, seguimos dividiendo sucesivamente ese cociente por el mismo número primo.
- Cuando no podamos hacer la división por ese número primo, lo hacemos por el siguiente primo que se pueda.
- Así sucesivamente hasta que el cociente final sea 1.
- El producto de todos los números primos por los que hemos ido dividiendo constituyen la descomposición factorial del número.
Halla la descomposición factorial de 90.
Solución:
Dividimos 90 entre el primer número primo por el que sea divisible. En este caso, por 2. (90:2=45) A continuación, procedemos a dividir 45, cociente de la anterior división, de igual forma. (45:3=15) Así sucesivamente hasta obtener 1 en el cociente (15:3=5; 5:5=1)
Los cocientes 2, 3, 3 y 5 son los factores que descomponen a 90.
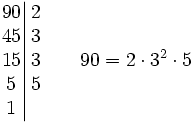
Mínimo común múltiplo
|
Ejercicios propuestos: Descomposición en factores. Mínimo común múltiplo. |