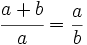Número áureo
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:11 7 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:28 7 sep 2016 Coordinador (Discusión | contribuciones) (→Razón áurea) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | ==Razón áurea== | + | ==El número áureo== |
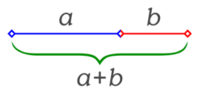
| - | [[Imagen:Image-Golden ratio line.png|200px|thumb|El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total <font color="green">'''''a+b'''''</font> es al segmento más largo <font color="blue">'''''a'''''</font>, como <font color="blue">'''''a'''''</font> es al segmento más corto <font color="red">'''''b'''''</font>.]] | + | {{Tabla75|celda2=[[Imagen:Image-Golden ratio line.png|200px|thumb|El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total <font color="green">'''''a+b'''''</font> es al segmento más largo <font color="blue">'''''a'''''</font>, como <font color="blue">'''''a'''''</font> es al segmento más corto <font color="red">'''''b'''''</font>.]] |
| - | {{p}} | + | |celda1= |
| + | El '''número áureo''', es un [[Números irracionales|número irracional]], representado por la letra griega phi φ (en minúscula) o Φ (en mayúscula) en honor al escultor griego Fidias, cuyo valor es: | ||
| + | |||
| + | <center><math>\varphi = \frac{1 + \sqrt{5}}{2} \approx 1,61803398874988...</math></center> | ||
| + | |||
| + | También se le conoce como '''número de oro''' o '''razón áurea''' o '''divina proporción''' (por la obra de Luca Pacioli, ''De Divina Proportione'', escrito entre 1496 y 1498). | ||
| + | |||
| + | {{Teorema|titulo=Origen del número áureo|enunciado=El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total ''a+b'' es al segmento más largo ''a'', como ''a'' es al segmento más corto ''b''. (Ver Fig.1) | ||
| + | |||
| + | <center><math>\cfrac{a+b}{a} = \frac{a}{b}</math></center> | ||
| + | |||
| + | |demo= | ||
| + | }} | ||
| + | }} | ||
| + | |||
| ==Rectángulo áureo== | ==Rectángulo áureo== | ||
| El '''rectángulo áureo''' (denominado también rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual a la '''razón áurea'''. Es decir, es aquél rectángulo que al substraer la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo dorado | El '''rectángulo áureo''' (denominado también rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual a la '''razón áurea'''. Es decir, es aquél rectángulo que al substraer la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo dorado | ||
Revisión de 19:28 7 sep 2016
El número áureo
El número áureo, es un número irracional, representado por la letra griega phi φ (en minúscula) o Φ (en mayúscula) en honor al escultor griego Fidias, cuyo valor es:
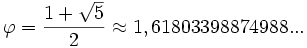 También se le conoce como número de oro o razón áurea o divina proporción (por la obra de Luca Pacioli, De Divina Proportione, escrito entre 1496 y 1498).  Origen del número áureo El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total a+b es al segmento más largo a, como a es al segmento más corto b. (Ver Fig.1)  Demostración: |  |
Rectángulo áureo
El rectángulo áureo (denominado también rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual a la razón áurea. Es decir, es aquél rectángulo que al substraer la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo dorado
