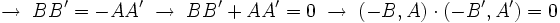Paralelismo y perpendicularidad en el plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:15 12 oct 2016 Coordinador (Discusión | contribuciones) (→Paralelismo) ← Ir a diferencia anterior |
Revisión de 19:15 12 oct 2016 Coordinador (Discusión | contribuciones) (→Perpendicularidad) Ir a siguiente diferencia → |
||
| Línea 38: | Línea 38: | ||
| {{Teorema|titulo=Proposición|enunciado=Dos rectas son perpendiculares si: | {{Teorema|titulo=Proposición|enunciado=Dos rectas son perpendiculares si: | ||
| - | *El producto escalar de sus '''vectores de dirección''' es cero: <math>\vec{d_1} \cdot \vec{d_2} = 0</math> | + | *El producto escalar de sus '''vectores de dirección''' es cero: {{sube|porcentaje=+20%|contenido=<math>\vec{d_1} \cdot \vec{d_2} = 0</math>}} |
| - | *El producto escalar de sus '''vectores normales''' es cero: <math>\vec{n_1} \cdot \vec{n_2} = 0</math> | + | *El producto escalar de sus '''vectores normales''' es cero: {{sube|porcentaje=+20%|contenido=<math>\vec{n_1} \cdot \vec{n_2} = 0</math>}} |
| *Sus '''pendientes''', <math>m\,</math> y {{sube|porcentaje=+20%|contenido=<math>m'\,</math>}}, cumplen que: {{sube|porcentaje=+20%|contenido=<math>m'=-\cfrac{1}{m}</math>}}. | *Sus '''pendientes''', <math>m\,</math> y {{sube|porcentaje=+20%|contenido=<math>m'\,</math>}}, cumplen que: {{sube|porcentaje=+20%|contenido=<math>m'=-\cfrac{1}{m}</math>}}. | ||
Revisión de 19:15 12 oct 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Paralelismo
Dos rectas son paralelas si tienen la misma dirección.
He aquí tres criterios para determinar si dos rectas son paralelas:
Proposición
Dos rectas son paralelas si:
- Sus vectores de dirección son proporcionales.
- Sus vectores normales son proporcionales.
- Sus pendientes coinciden.
Demostración:
- La primera afirmación es inmediata ya que dos rectas son paralelas si tienen la misma dirección y sabemos que dos vectores tiene la misma dirección si son proporcionales.
- Si los vectores normales son proporcionales es porque tienen la misma dirección, entonces los vectores directores también la tienen y también serán proporcionales.
- Para la segunda afirmación, recordemos que la pendiente de una recta coincide con la tangente del ángulo que forma con el eje de abscisas, por tanto, si dos rectas tienen la misma pendiente, las tangentes de los ángulos que forman, serán iguales. Ahora, si las tangentes de dos ángulos son iguales, los ángulos o son iguales o difieren en 180º. En ambos casos las rectas tienen la misma inclinación.
Perpendicularidad
Dos rectas son perpendiculares si sus vectores de dirección son ortogonales.
He aquí tres criterios para determinar si dos rectas son perpendiculares:
Proposición
Dos rectas son perpendiculares si:
- El producto escalar de sus vectores de dirección es cero:
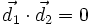
- El producto escalar de sus vectores normales es cero:
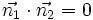
- Sus pendientes,
 y
y 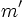 , cumplen que:
, cumplen que: 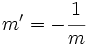 .
.
Demostración:
- La primera afirmación es inmediata ya que dos rectas son perpendiculares si sus vectores de dirección son ortogonales y esto ocurre cuando el producto escalar de ambos es cero.
- La segunda también ya que si los vectores normales son ortogonales, también lo son los vectores directores.
- Para la tercera afirmación: Dada una recta
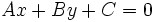 , sabemos que
, sabemos que 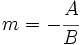 es la pendiente de esa recta y que
es la pendiente de esa recta y que 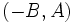 es su vector de dirección.
es su vector de dirección.
Sea 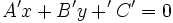 , otra recta, con
, otra recta, con 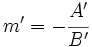 su pendiente, y
su pendiente, y 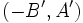 su vector de dirección.
su vector de dirección.
Supongamos que 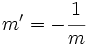 . Sustituyendo:
. Sustituyendo:
Traduciendo ésto a coordenadas:
Proposición
Dos rectas con vectores de dirección 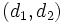 y
y 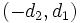 son perpendiculares.
son perpendiculares.
Demostración:
Es inmediato a partir de lo dicho antes ya que el producto escalar de estos dos vectores es cero.
En esta escena podrás practicar con la posición relativa de dos rectas.
Ejercicios propuestos
|
Ejercicios propuestos: Paralelismo y perpendicularidad |