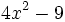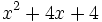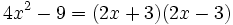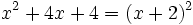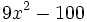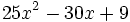Plantilla:Factorización de polinomios usando identidades notables
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:13 25 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:30 1 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 10: | Línea 10: | ||
| a) <math>4x^2-9=(2x+3)(2x-3) \!</math> | a) <math>4x^2-9=(2x+3)(2x-3) \!</math> | ||
| b) <math>x^2+4x+4 = (x+2)^2\!</math> | b) <math>x^2+4x+4 = (x+2)^2\!</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplos 1: Factorización de una diferencia de cuadrados | ||
| + | |duracion=4'22" | ||
| + | |sinopsis=2 ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=tABhBMtBmSY&index=49&list=PL9B9AC3136D2D4C45 | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 16:30 1 may 2017
Mediante productos notables podemos transformar un polinomio en un producto de factores.
2 ejemplos.