Plantilla:Número de soluciones de un sistema
De Wikipedia
| Revisión de 09:46 1 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:52 1 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 20: | Línea 20: | ||
| *Si las dos rectas son coincidentes: Infinitas soluciones (S.C.I.) | *Si las dos rectas son coincidentes: Infinitas soluciones (S.C.I.) | ||
| *Si las rectas son paralelas: 0 soluciones (S.I.) | *Si las rectas son paralelas: 0 soluciones (S.I.) | ||
| + | }} | ||
| + | |||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás ver la representación gráfica de los distintos tipos de sistemas según el número de soluciones. | ||
| + | |enlace=[https://ggbm.at/hhAmGM39 Actividad: Número de soluciones de un sistema] | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 09:52 1 nov 2016
- Un sistema es compatible si tiene solución e incompatible si no la tiene.
- Un sistema es determinado si tiene un número finito de soluciones e indeterminado si tiene infinitas soluciones.
- Usaremos las siguientes siglas para abreviar:
- S.C.D. : Sistema Compatible Determinado (un número finito de soluciones)
- S.C.I. : Sistema Compatible Indeterminado (infinitas soluciones)
- S.I. : Sistema Incompatible (sin solución)
Número de soluciones de un sistema 2x2 de ecuaciones lineales
Un sistema 2x2 de ecuaciones lineales puede ser:
- Compatible determinado (S.C.D.): 1 solución
- Compatible indeterminado (S.C.I.): Infinitas soluciones.
- Incompatible (S.I): 0 soluciones.
En efecto, razonando a partir de sus representaciones gráficas:
- Si las dos rectas se cortan en un punto: 1 solución (S.C.D.)
- Si las dos rectas son coincidentes: Infinitas soluciones (S.C.I.)
- Si las rectas son paralelas: 0 soluciones (S.I.)
En esta escena podrás ver la representación gráfica de los distintos tipos de sistemas según el número de soluciones.
En la siguiente actividad veremos un ejemplo de cada uno de los tres casos anteriores.
|
Actividad Interactiva: Soluciones de un sistema
Actividad 1: Sistema incompatible.
Actividad: Dado el siguiente sistema 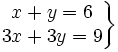
Actividad 2: Sistema compatible indeterminado.
Actividad: Dado el siguiente sistema 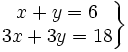 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados:
Actividad 3: Sistema compatible determinado.
Actividad: Dado el siguiente sistema 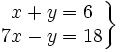 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados: |

