Tendencias de una función (3ºESO Académicas)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:23 4 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:24 4 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 12: | Línea 12: | ||
| {{Caja Amarilla | {{Caja Amarilla | ||
| |texto= | |texto= | ||
| - | Decimos que una función <math>y=f(x)\;</math> '''tiende''' a un valor <math>y_o\;</math>, al aumentar la variable independiente indefinidamente, si los valores de la variable dependiente <math>y\;</math> se acercan a <math>y_o\;</math> cuando la variable <math>x\;</math> toma valores suficientemente grandes. | + | Decimos que una función <math>y=f(x)\;</math> '''tiende''' a un valor <math>y_o\;</math> (al aumentar la variable <math>x\;</math> indefinidamente) si los valores de la variable dependiente <math>y\;</math> se acercan a <math>y_o\;</math> cuando la variable <math>x\;</math> toma valores suficientemente grandes. |
| Simbólicamente: | Simbólicamente: | ||
Revisión de 19:24 4 nov 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 150)
Tendencia de una función
Decimos que una función 
tiende a un valor 
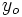(al aumentar la variable 
indefinidamente) si los valores de la variable dependiente 
se acercan a 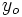cuando la variable toma valores suficientemente grandes.
Simbólicamente:
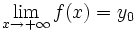
Tendencia de una función Descripción: En esta escena podrás estudiar la tendencia de una función que relaciona la temperatura de un recipiente de agua que se va enfriando y el tiempo que ha transcurrido.
Ejercicios propuestos
 Ejercicios propuestos: Las funciones y sus gráficas (Pág. 150)
|
