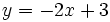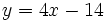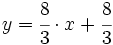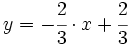Ecuaciones de la recta
De Wikipedia
| Revisión de 13:53 9 nov 2016 Coordinador (Discusión | contribuciones) (→Ecuación de la recta que pasa por dos puntos) ← Ir a diferencia anterior |
Revisión de 13:56 9 nov 2016 Coordinador (Discusión | contribuciones) (→Ecuación punto-pendiente de una recta) Ir a siguiente diferencia → |
||
| Línea 58: | Línea 58: | ||
| En la ecuación punto-pendiente: | En la ecuación punto-pendiente: | ||
| <center><math>y-y_o=m(x-x_o)\;\!</math></center>{{p}} | <center><math>y-y_o=m(x-x_o)\;\!</math></center>{{p}} | ||
| - | sustituimos <math>m=3</math>, <math>x_o=-2</math>, <math>y_o=4</math>, obteniendo: | + | sustituimos <math>m=3\;</math>, <math>x_o=-2\;</math>, <math>y_o=4\;</math>, obteniendo: |
| {{Caja |contenido=<math>y-4=3(x+2)\;\!</math>}} | {{Caja |contenido=<math>y-4=3(x+2)\;\!</math>}} | ||
| }}{{p}} | }}{{p}} | ||
Revisión de 13:56 9 nov 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Ejercicios Ecuación pto-pendiente Ecuaciones de la recta | WIRIS Geogebra Calculadora Función lineal Recta |
Tabla de contenidos |
Ecuación explícita de una recta
La ecuación explícita de la recta viene dada por la ya conocida expresión:
|
|
Ecuación general o implícita de una recta
La ecuación de la recta también la podemos expresar con todos los términos en lado izquierdo de la ecuación, igualados a cero. Es lo que se denomina:Ecuación general o implícita de la recta:
|
|
Ejemplo: Ecuación general
Halla la ecuación general de la recta 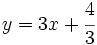 .
.
Nos dan la ecuación explícita:
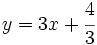
Tenemos que pasar todos los términos de la ecuación al lado izquierdo y ordenarlos:
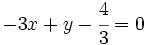
Opcionalmente, podemos quitar denominadores:
|
|
Ecuación punto-pendiente de una recta
Una recta queda perfectamente determinada por su inclinación y por un punto contenido en ella. Esto nos permite dar el siguiente resultado:
Ecuación punto-pendiente
Sea 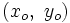 un punto de una recta y
un punto de una recta y  su pendiente, entonces su ecuación viene dada por:
su pendiente, entonces su ecuación viene dada por:
|
|
expresión que se denomina ecuación punto-pendiente de la recta.
Para comprobar que esta es la ecuación de la recta, comprobaremos que su pendiente es  y que pasa por el punto dado
y que pasa por el punto dado 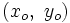 .
En efecto:
.
En efecto:
- Si desarrollamos la expresión de la ecuación punto-pendiente, se obtiene:
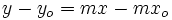
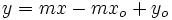
de donde se observa que el coeficiente e la x es  , y por tanto, la pendiente de la recta.
, y por tanto, la pendiente de la recta.
- Si sustituimos el punto
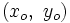 en la ecuación punto-pendiente, es decir, hacemos
en la ecuación punto-pendiente, es decir, hacemos 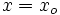 e
e 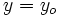 , se obtiene
, se obtiene
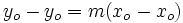
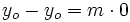
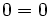
Ejemplo: Ecuación punto-pendiente
Halla la ecuación punto-pendiente de la recta que pasa por el punto (-2, 4) y tiene pendiente 3.
En la ecuación punto-pendiente:
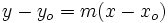
sustituimos 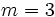 ,
, 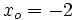 ,
, 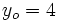 , obteniendo:
, obteniendo:
|
|
|
Actividad Interactiva: Ecuación punto-pendiente
1. Halla la ecuación de la recta conocida la pendiente y un punto.
Actividad: Como se conoce la pendiente, sólo hay que determinar la ordenada en el origen de la recta y = mx + k. a) Tienes que escribir el valor de k para determinar la ecuación de la recta que pasa por el punto amarillo y tiene de pendiente el valor indicado, m. El pulsador azul de la ayuda la activa y el rojo la desactiva. Con la ayuda activada no cuenta los aciertos. Si aciertas verás la expresión de la función con color naranja, si no aciertas verás la recta correspondiente de color rojizo. Después de cada acierto pulsa el botón animar para que se salga una nueva recta. |
Ecuación de la recta que pasa por dos puntos
Dos puntos determinan una única recta que pasa por ellos. Veamos como se obtiene su ecuación:
Procedimiento
Sean 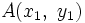 y
y 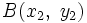 dos puntos de una recta. Para hallar su ecuación procederemos como sigue:
dos puntos de una recta. Para hallar su ecuación procederemos como sigue:
- Con los dos punto hallaremos la pendiente:
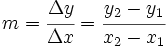
- A continuación podemos seguir dos caminos:
- a) Usar la ecuación punto-pendiente: con uno cualquiera de los dos puntos y con la pendiente que acabamos de calcular.
- b) Usar la ecuación explícita,
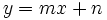 : sustituyendo las coordenadas de uno de los dos puntos y el valor de la pendiente, despejaremos el valor de
: sustituyendo las coordenadas de uno de los dos puntos y el valor de la pendiente, despejaremos el valor de  .
.
Ejemplo: Ecuación de la recta que pasa por dos puntos
Halla la ecuación de la recta que pasa por los puntos (2, 4) y (-3, 5).
Hallamos la pendiente:

- Primer método: Usando la ecuación punto-pendiente con el punto (2,4) y la pendiente


- Segundo método: Usando la ecuación explícita con el punto (2,4) y la pendiente

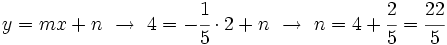
- de donde:
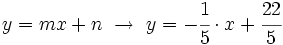
|
Actividades Interactivas: Ecuación de la recta que pasa por dos puntos
1. Ecuación punto-pendiente de la recta que pasa por dos puntos.
Actividad: Por dos puntos distintos pasa una única recta. Si los puntos son 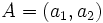 y y 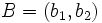 la ecuación de la recta que pasa por ellos es: la ecuación de la recta que pasa por ellos es:
con a) Calcula la ecuación de la recta que pasa por los puntos (2,-3) y (5, 4) y compruébala en la siguiente escena:
2. Ecuaciones continua y general de la recta que pasa por dos puntos.
Actividad: La ecuación continua de la recta que pasa por los puntos 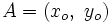 y y 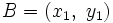 es: es:
a) Calcula la ecuación continua y general de la recta que pasa por los puntos (-1,3) y (1, 2) y compruébala en la siguiente escena: b) Comprueba si los puntos A(1,0), B(2,1) y C(3,3) están o no alineados. (Sugerencia: Calcula la recta que pasa por A y B, y comprueba que C pertenece a ella.) |
Ejercicios
|
Ejercicios: Ecuaciones de la recta 1. Halla la ecuación de las siguientes rectas:
Solución:
2. Averigua si los puntos (0,3), (3,1) y (9,-4) están alineados. Solución: Se halla la ecuación de la recta que pasa por los dos primeros puntos y se comprueba que el tercer punto no verifica la ecuación. Por tanto no están alineados. |
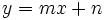
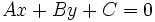
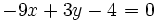
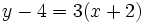
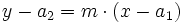
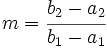 .
.
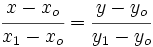
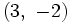 .
.
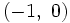 y
y 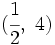 .
.
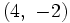 y es paralela a la recta
y es paralela a la recta 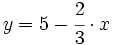 .
.