Función cuadrática (3ºESO Académicas)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:52 13 nov 2016 Coordinador (Discusión | contribuciones) (→Función cuadrática tipo) ← Ir a diferencia anterior |
Revisión de 11:18 13 nov 2016 Coordinador (Discusión | contribuciones) (→Función cuadrática tipo) Ir a siguiente diferencia → |
||
| Línea 18: | Línea 18: | ||
| ==Representación gráfica de la función cuadrática== | ==Representación gráfica de la función cuadrática== | ||
| ===Función cuadrática tipo=== | ===Función cuadrática tipo=== | ||
| + | {{Tabla75|celda2=[[Imagen=graf_x_2.png|center]] | ||
| + | |celda1= | ||
| Empezaremos representando la función cuadrática mas sencilla, que llamaremos función cuadrática tipo, cuya ecuación es: | Empezaremos representando la función cuadrática mas sencilla, que llamaremos función cuadrática tipo, cuya ecuación es: | ||
| <center><math>y=x^2\;</math></center> | <center><math>y=x^2\;</math></center> | ||
| - | Para ello haremos una tabla de valores: | + | Para ello haremos una tabla de valores, a aprtir de la cual dibujaremos su gráfica: |
| [[Imagen:tabla_x_2.png|center]] | [[Imagen:tabla_x_2.png|center]] | ||
| - | + | }} | |
| {{p}} | {{p}} | ||
Revisión de 11:18 13 nov 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 171)
Función cuadrática
Una función cuadrática es aquella cuya expresión analítica es o puede ponerse como una ecuación polinómica de segundo grado:
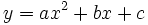 |
con 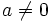 .
.
Representación gráfica de la función cuadrática
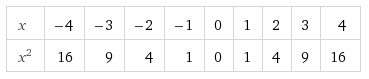
Función cuadrática tipo
Empezaremos representando la función cuadrática mas sencilla, que llamaremos función cuadrática tipo, cuya ecuación es:
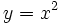 Para ello haremos una tabla de valores, a aprtir de la cual dibujaremos su gráfica: | center |
Propiedades
La representación gráfica de la función cudrática recibe el nombre de parábola y tiene las siguientes propiedades:
- La parábola es simétrica respecto de un eje paralelo al eje Y, que llamaremos eje de la parábola.
- El eje de la parábola corta a la parábola por un punto llamado vértice.
- El eje de la parábola la divide en dos partes denominadas ramas.
- Si
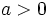 , la parábola tiene las ramas hacia arriba.
, la parábola tiene las ramas hacia arriba.
- Si
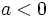 , la parábola tiene las ramas hacia abajo.
, la parábola tiene las ramas hacia abajo.
- Si
- Cuanto mayor es
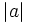 , más estilizada es la parábola.
, más estilizada es la parábola.
- Dos parábolas con el mismo coeficiente
 , tienen formas idénticas aunque están situadas en posiciones distintas.
, tienen formas idénticas aunque están situadas en posiciones distintas.
Ejercicios propuestos
|
Ejercicios propuestos: Estudio conjunto de dos funciones lineales |