Plantilla:Inecuaciones con una incógnita
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:37 15 nov 2016 Coordinador (Discusión | contribuciones) (→Resolución de inecuaciones con una incógnita) ← Ir a diferencia anterior |
Revisión de 12:37 15 nov 2016 Coordinador (Discusión | contribuciones) (→Resolución de inecuaciones con una incógnita) Ir a siguiente diferencia → |
||
| Línea 13: | Línea 13: | ||
| {{p}} | {{p}} | ||
| ===Resolución de inecuaciones con una incógnita=== | ===Resolución de inecuaciones con una incógnita=== | ||
| - | {{teorema_sin_demo|titulo=Procedimiento|enunciado=Para resolver las inecuacines con una incógnita podemos utilizar dos métodos: | + | {{teorema_sin_demo|titulo=Procedimiento|enunciado=Para resolver las inecuaciones con una incógnita podemos utilizar dos métodos: |
| *El '''método algebraico''' que consiste en despejar la incógnita usando las reglas para trabajar con desigualdades antes mencionadas. | *El '''método algebraico''' que consiste en despejar la incógnita usando las reglas para trabajar con desigualdades antes mencionadas. | ||
Revisión de 12:37 15 nov 2016
- Una inecuación con una incógnita es una desigualdad entre expresiones matemáticas con una sola variable o incógnita.
- Una solución de una inecuación con una incógnita,
, es un valor de la variable que hace que se cumpla la desigualdad.
- Resolver una inecuación consiste en hallar todas sus soluciones. Habitualmente son infinitas y se expresan mediante intervalos de la recta real, aunque tambien puede ser finitas o no existir.
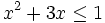es una inecuación cuadrática no estricta con una incógnita.
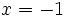es una solución de la inecuación anterior porque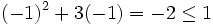 
Resolución de inecuaciones con una incógnita
Procedimiento
Para resolver las inecuaciones con una incógnita podemos utilizar dos métodos:
- El método algebraico que consiste en despejar la incógnita usando las reglas para trabajar con desigualdades antes mencionadas.
- El método gráfico que se apoya en el estudio del signo de una función polinómica. En este método, primero se pasan todos los términos al lado izquierdo de la inecuación, dejando el lado derecho cero. A continuación, se estudia el signo del polinomio que queda en el lado izquierdo.
