Plantilla:Ángulos en un polígono de n lados
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:51 24 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:57 24 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| *Si además el polígono es regular, al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n. | *Si además el polígono es regular, al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n. | ||
| - | {{p}} | + | }} |
| - | En la siguiente escena de Geogebra puedes ver el procedimiento para el caso de polígonos regulares, que es prácticamente lo mismo.}} | + | |
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
Revisión de 19:57 24 nov 2016
Propiedad
- La suma de los ángulos interiores de un polígono de
lados es igual a 
.
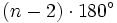- Si el polígono de lados es regular, cada ángulo interior mide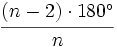
Demostración:
- Desde un vértice cualquiera del polígono se pueden trazar n-3 diagonales que dividen al polígono en n-2 triángulos. Sumando los ángulos de todos esos triángulos se obtiene la fórmula, ya que la suma de los ángulos de cada triángulo es 180º.
- Si además el polígono es regular, al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n.
Ángulos en los polígonos regulares Descripción: En esta escena podrás ver los ángulos central, interior y exterior de un polígono regular de hasta 20 lados.
