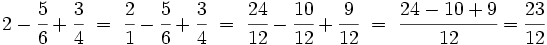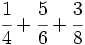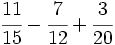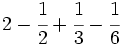Fracciones: Suma y resta (1º ESO)
De Wikipedia
| Revisión de 22:16 7 may 2017 Coordinador (Discusión | contribuciones) (→Suma y resta de fracciones con el mismo denominador) ← Ir a diferencia anterior |
Revisión de 22:18 7 may 2017 Coordinador (Discusión | contribuciones) (→Suma y resta de fracciones con el mismo denominador) Ir a siguiente diferencia → |
||
| Línea 32: | Línea 32: | ||
| |sinopsis=Suma o resta de fracciones con el mismo denominador. | |sinopsis=Suma o resta de fracciones con el mismo denominador. | ||
| - | |url1=https://www.youtube.com/watch?v=LVHo5xvsvO0}} | + | |url1=https://www.youtube.com/watch?v=antZqj9ePys |
| + | }} | ||
| {{p}} | {{p}} | ||
Revisión de 22:18 7 may 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 138)
Suma y resta de fracciones con el mismo denominador
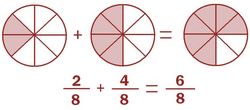
Procedimiento Para sumar o restar fracciones con el mismo denominador, sumamos o restamos los numeradores y dejamos el mismo denominador Suma o resta de fracciones con el mismo denominador. Suma y resta de fracciones con el mismo denominador. Suma y resta de fracciones con el mismo denominador. |
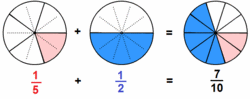
Suma y resta de fracciones con distinto denominador
Procedimiento Para sumar o restar fracciones con distinto denominador, primero se reducen las fracciones a común denominador y luego se procede como en el caso en el que las fracciones tienen el mismo denominador. |
Otro método para sumar o restar fracciones fácil de recordar pero que requiere simplificar más.
Suma y resta de fracciones con distinto denominador.
Suma y resta de fracciones con distinto denominador.
Suma y resta de fracciones con distinto denominador.
Suma de fracciones por el método del m.c.m.
Suma y resta de fracciones por el método del m.c.m.
Suma y resta de fracciones. Propiedades.
Suma y resta de fracciones con o sin paréntesis.
Ejercicios propuestos
|
Ejercicios propuestos: Suma y resta de fracciones |
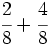 b)
b) 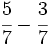
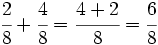
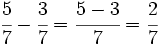
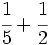 b)
b) 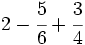
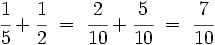 (Ver Fig. 2)
(Ver Fig. 2)