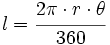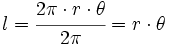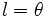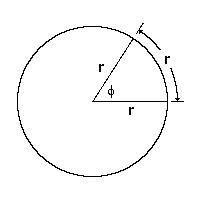Plantilla:El radian
De Wikipedia
| Revisión de 08:33 15 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 5: | Línea 5: | ||
| En la figura adjunta el ángulo <math>\phi \,</math> mide un radián porque abarca un arco que mide igual que el radio de la circunferencia. | En la figura adjunta el ángulo <math>\phi \,</math> mide un radián porque abarca un arco que mide igual que el radio de la circunferencia. | ||
| {{p}} | {{p}} | ||
| + | El radian se usa también en Física. Por ejemplo, la velocidad angular se suele medir en radianes por segundo (rad/s). | ||
| + | {{p}} | ||
| + | {{Nota|titulo=Utilidad del radián:|texto= | ||
| La utilidad de la medida en radianes frente a otras medidas de ángulos, es que ayuda a simplificar muchas fórmulas trigonométricas. | La utilidad de la medida en radianes frente a otras medidas de ángulos, es que ayuda a simplificar muchas fórmulas trigonométricas. | ||
| + | |||
| + | Por ejemplo, la fórmula para hallar la longitud de un arco de circunferencia de radio ''r'' correspondiente a un ángulo <math>\theta</math> (en grados sexagesimales), viene dada por la fórmula: | ||
| + | |||
| + | :<math>l=\cfrac{2\pi \cdot r \cdot \theta}{360}</math> | ||
| + | |||
| + | Ahora, si <math>\theta</math> viene dado en radianes, la fórmula es: | ||
| + | |||
| + | :<math>l=\cfrac{2\pi \cdot r \cdot \theta}{2\pi}=r \cdot \theta</math> | ||
| + | |||
| + | Si además trabajamos con el círculo unidad (''r = 1''): | ||
| + | |||
| + | :<math>l= \theta\;</math> | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | El radian se usa también en Física. Por ejemplo, la velocidad angular se suele medir en radianes por segundo (rad/s). | ||
| }} | }} | ||
Revisión actual
El radián (simbolizado rad) se define como el ángulo que abarca un arco de circunferencia cuya longitud es igual a la del radio de la propia circunferencia. En la figura adjunta el ángulo El radian se usa también en Física. Por ejemplo, la velocidad angular se suele medir en radianes por segundo (rad/s).  La utilidad de la medida en radianes frente a otras medidas de ángulos, es que ayuda a simplificar muchas fórmulas trigonométricas. Por ejemplo, la fórmula para hallar la longitud de un arco de circunferencia de radio r correspondiente a un ángulo θ (en grados sexagesimales), viene dada por la fórmula: Ahora, si θ viene dado en radianes, la fórmula es: Si además trabajamos con el círculo unidad (r = 1): | 
|
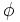mide un radián porque abarca un arco que mide igual que el radio de la circunferencia.
