Plantilla:Factorización de polinomios usando identidades notables
De Wikipedia
| Revisión de 06:36 29 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:36 29 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| |sol= | |sol= | ||
| - | a) <math>4x^2-9=(2x+3)(2x-3) \!</math> | + | '''Solución:''' |
| - | b) <math>x^2+4x+4 = (x+2)^2\!</math> | + | |
| + | '''a)''' Al tratarse de un binomio cuyos términos están restando, sólo podemos ponerlo como diferencia de cuadrados. Extrayendo las raíces cuadradas de cada término tenemos: | ||
| + | |||
| + | <math>\left . \begin{matrix}\sqrt{4x^2}=2x \\ \sqrt{9}=3 \end{matrix} \right \} \ \rightarrow \ 4x^2-9=(2x+3)(2x-3) \!</math> | ||
| + | '''b)''' Al tratarse de un trinomio, buscaremos dos de sus términos que sean cuadrados perfectos y calcularemos su raíz cuadrada: | ||
| + | |||
| + | <math>\left . \begin{matrix}\sqrt{x^2}=x \\ \sqrt{4}=2 \end{matrix} \right \} \ \rightarrow \ x^2+4x+4 =(x+2)^2 \!</math> | ||
| + | |||
| + | Para confirmar que esa es la factorización, comprobaremos que el doble producto del primero por el segundo es igual al otro término: | ||
| + | |||
| + | :<math>2 \cdot x \cdot 2 =4x\;</math> | ||
| + | |||
| + | En efecto, luego esa es la factorización. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 07:36 29 may 2017
Mediante productos notables podemos transformar un polinomio en un producto de factores.
Ejemplos: Factorización de polinomios usando productos notables
Factoriza:
- a)
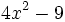
- b)
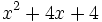
Solución:
a) Al tratarse de un binomio cuyos términos están restando, sólo podemos ponerlo como diferencia de cuadrados. Extrayendo las raíces cuadradas de cada término tenemos:
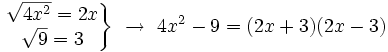 b) Al tratarse de un trinomio, buscaremos dos de sus términos que sean cuadrados perfectos y calcularemos su raíz cuadrada:
b) Al tratarse de un trinomio, buscaremos dos de sus términos que sean cuadrados perfectos y calcularemos su raíz cuadrada:
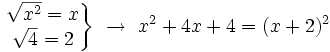
Para confirmar que esa es la factorización, comprobaremos que el doble producto del primero por el segundo es igual al otro término:
Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: | Factoriza: Factoriza: Factoriza: Factoriza los siguientes polinomos usando diferencias de cuadrados:
Factoriza los siguientes polinomos usando diferencias de cuadrados:
Factoriza:
Factoriza: Factoriza: Factoriza: |
Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: | Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza los siguientes polinomios usando trinomios cuadrado perfecto:
Factoriza los siguientes polinomios usando trinomios cuadrado perfecto:
Factoriza los siguientes polinomios usando trinomios cuadrado perfecto:
Factoriza:
Factoriza: Factoriza: Factoriza: Factoriza: Averigua el valor de "c" y "d" de manera que Averigua el valor de "c" y "d" de manera que |
Factoriza: 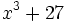
Factoriza: 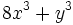
Factoriza: 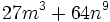
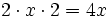
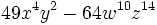
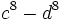
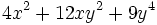
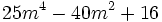
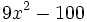
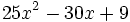
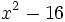
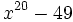
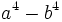
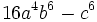
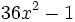
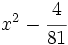
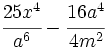
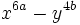
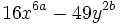
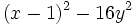

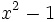
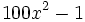
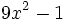
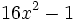
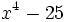
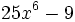
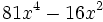
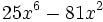
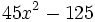
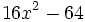

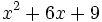
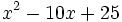
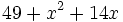
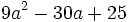

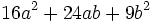
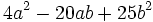
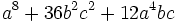
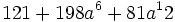
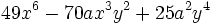
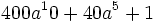
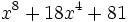
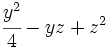
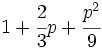
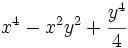
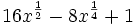
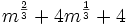
![\sqrt[3]{m^2}-6\sqrt[3]{m}+9\;](/wikipedia/images/math/a/2/a/a2a527f84cd9528ace07b344292c0c0b.png)
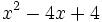
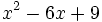
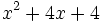
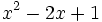
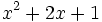

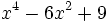
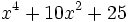
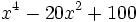
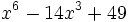
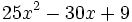
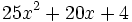
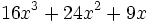
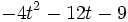
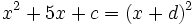 .
.

