Ecuaciones de segundo grado (3ºESO Académicas)
De Wikipedia
| Revisión de 10:35 6 jun 2017 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) ← Ir a diferencia anterior |
Revisión de 11:01 6 jun 2017 Coordinador (Discusión | contribuciones) (→Resolución de problemas mediante ecuaciones de segundo grado) Ir a siguiente diferencia → |
||
| Línea 158: | Línea 158: | ||
| [[Imagen:red_star.png|12px]] 1, 2 | [[Imagen:red_star.png|12px]] 1, 2 | ||
| }} | }} | ||
| + | {{p}} | ||
| + | ===Actividades y videotutoriales=== | ||
| + | {{Actividades y videotutoriales: ecuación de segundo grado}} | ||
| {{p}} | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión de 11:01 6 jun 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 108)
Ecuación de segundo grado
- Una ecuación de segundo grado con una incógnita,
 , es aquella que tiene o se puede reducir a la siguiente expresión, que llamaremos forma general.
, es aquella que tiene o se puede reducir a la siguiente expresión, que llamaremos forma general.
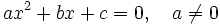
- Si algún coeficiente,"b" o "c", es cero la ecuación diremos que es incompleta. En caso contrario diremos que es completa.
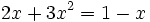 es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general:
es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general: 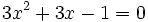
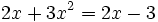 es una ecuación de segundo grado incompleta, ya que se puede reducir a la siguiente forma general:
es una ecuación de segundo grado incompleta, ya que se puede reducir a la siguiente forma general: 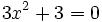
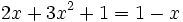 es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general:
es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general: 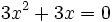
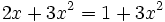 no es una ecuación de segundo grado, ya que al reducirla resulta una ecuación de primer grado:
no es una ecuación de segundo grado, ya que al reducirla resulta una ecuación de primer grado: 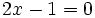
Definición de ecuación de segundo grado.
Actividades en la que aprenderás a identificar los coeficientes de una ecuación de segundo grado y a determinar si es completa o incompleta.
El siguiente videotutorial condensa casi todo lo que se va a tratar en este tema:
- Definición de ecuación de segundo grado.
- Fórmula para su resolución con su demostración.
- Definición de discriminante de una ec. de segundo grado y su relación con el número de soluciones de ésta y con ejemplos de cada caso.
- Factorización del polinomio de segundo grado a partir de las soluciones o raíces de la ecuación de segundo grado.
- Propiedades del producto y la suma de las raíces de la ecuación con su demostración.
- Ecuaciones de segundo grado incompletas.
Ecuación de segundo grado completa
Fórmula general
Las soluciones de la ecuación de segundo grado
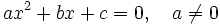
son:
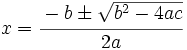
donde el signo 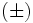 significa que una solución se obtiene con el signo
significa que una solución se obtiene con el signo 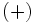 y otra con el signo
y otra con el signo 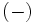 .
.
A continuación tienes la demostración en videtutorial y por escrito:
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Demostración:
1. Se divide la ecuación por  :
:
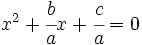
2. Se multiplica y divide por  el coeficiente de la
el coeficiente de la  :
:
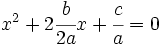
3. Se suma a los dos miembros de la igualdad 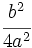 :
:
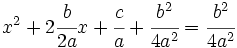
4. Se pasa restando a la derecha  :
:
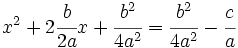
5. Observando que el lado izquierdo es el desarrollo de 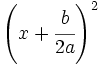 :
:
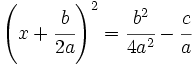
6. Se extrae la raíz cuadrada en ambos miembros:
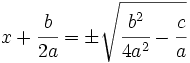
7. Se despeja x:
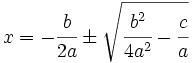
8. Se simplifica la expresión:
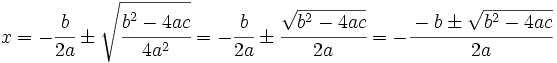
En la escena, pulsa "Inicio" para ver otros ejemplos.
Cómo utilizar la fórmula general de la ecuación de segundo grado.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Tutorial en el que se explica la resolución de ecuaciones de 2º grado aplicando la fórmula general de resolución.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Escribe en forma general e identifica los coeficientes "a", "b", y "c": 6x2 + 3 = 2x − 6.
Resuelve usando la fórmula: − x2 + 8x = 1.
Resuelve usando la fórmula: − 3x2 + 10x − 3 = 0.
Resuelve usando la fórmula: − 7q2 + 2q + 9 = 0.
Actividades en la que aprenderás a resolver ecuaciones de segundo grado completas.
Actividades en la que aprenderás a resolver ecuaciones de segundo grado completas.
Resolver ecuaciones de segundo grado completas.
Ejercicios de autoevaluación sobre ecuaciones de segundo grado completas.
- Pulsa el botón "Ejercicio" para obtener una ecuación.
- Copia la ecuación en tu cuaderno y halla sus soluciones.
- Escribe el "tipo de solución" y las soluciones en los cuadros correspondientes. Luego pulsa el botón "Solución".
Ejercicios resueltos sobre ecuaciones de segundo grado completas.
Número de soluciones de la ecuación de segundo grado
Llamamos discriminante de una ecuación de segundo grado, 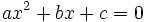 , al número:
, al número:
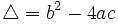
Proposición
Sea  el discriminante de una ecuación de segundo grado:
el discriminante de una ecuación de segundo grado:
- Si
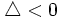 , la ecuación no tiene solución.
, la ecuación no tiene solución.
- Si
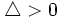 , la ecuación tiene dos soluciones.
, la ecuación tiene dos soluciones.
- Si
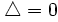 , la ecuación tiene una solución (doble).
, la ecuación tiene una solución (doble).
La demostración es inmediata teniendo en cuenta la fórmula para la resolución de la ecuación de segundo grado:
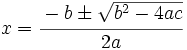
ya que, lo que hay en el radicando, es precisamente el discriminante. Por tanto,
- Si su signo es positivo, la raíz existe y da lugar a dos soluciones distintas.
- Si su signo es negativo, la raíz no existe y no hay ninguna solución.
- Si es cero, la raíz vale cero, y hay dos soluciones iguales (solución doble).
Número de soluciones de una ecuación de 2º grado. Discriminante.
Halla el discriminante para determinar el número de raíces de la ecuación 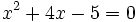 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 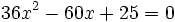 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 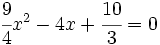 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 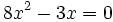 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 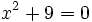 .
.
Determinar el número de soluciones de la ecuación 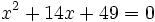 .
.
Actividades en la que aprenderás a calcular el discriminante de una ecuación de segundo grado y su utilidad para determinar el número de soluciones de la misma.
Calcula el número de soluciones de una ecuación de segundo grado:
- Pulsa el botón "Ejercicio" para obtener una ecuación.
- Copia la ecuación en tu cuaderno y calcula su discriminante.
- Teniendo en cuenta el valor del discriminante, determina cuántas soluciones tiene.
- Escribe el número de soluciones en el cuadro "Número de soluciones" y pulsa el botón "Solución".
Ejercicios de autoevaluación sobre las soluciones de las ecuaciones de segundo grado.
Ejercicios de autoevaluación sobre las soluciones de las ecuaciones de segundo grado.
Llamamos discriminante de una ecuación de segundo grado, 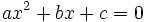 , al número:
, al número:
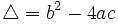
Proposición
Sea  el discriminante de una ecuación de segundo grado:
el discriminante de una ecuación de segundo grado:
- Si
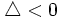 , la ecuación no tiene solución.
, la ecuación no tiene solución.
- Si
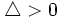 , la ecuación tiene dos soluciones.
, la ecuación tiene dos soluciones.
- Si
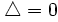 , la ecuación tiene una solución (doble).
, la ecuación tiene una solución (doble).
La demostración es inmediata teniendo en cuenta la fórmula para la resolución de la ecuación de segundo grado:
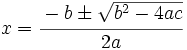
ya que, lo que hay en el radicando, es precisamente el discriminante. Por tanto,
- Si su signo es positivo, la raíz existe y da lugar a dos soluciones distintas.
- Si su signo es negativo, la raíz no existe y no hay ninguna solución.
- Si es cero, la raíz vale cero, y hay dos soluciones iguales (solución doble).
Número de soluciones de una ecuación de 2º grado. Discriminante.
Halla el discriminante para determinar el número de raíces de la ecuación 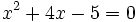 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 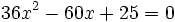 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 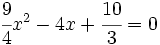 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 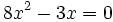 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 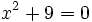 .
.
Determinar el número de soluciones de la ecuación 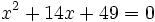 .
.
Actividades en la que aprenderás a calcular el discriminante de una ecuación de segundo grado y su utilidad para determinar el número de soluciones de la misma.
Calcula el número de soluciones de una ecuación de segundo grado:
- Pulsa el botón "Ejercicio" para obtener una ecuación.
- Copia la ecuación en tu cuaderno y calcula su discriminante.
- Teniendo en cuenta el valor del discriminante, determina cuántas soluciones tiene.
- Escribe el número de soluciones en el cuadro "Número de soluciones" y pulsa el botón "Solución".
Ejercicios de autoevaluación sobre las soluciones de las ecuaciones de segundo grado.
Ejercicios de autoevaluación sobre las soluciones de las ecuaciones de segundo grado.
Ejercicios propuestos
|
Ejercicios propuestos: Resolución de ecuaciones de segundo grado |
Ecuaciones de segundo grado incompletas
Una ecuación de segundo grado, 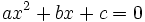 , es incompleta, si
, es incompleta, si 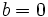 ó
ó 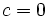 :
:
- Si
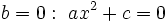
- Si
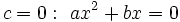
Resolución de las ecuaciones de segundo grado incompletas
- En el caso
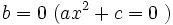 , las soluciones se obtienen despejando
, las soluciones se obtienen despejando  :
:
- En el caso
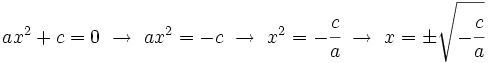
- En el caso
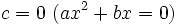 , las soluciones se obtienen sacando factor común e igualando a cero cada factor:
, las soluciones se obtienen sacando factor común e igualando a cero cada factor:
- En el caso
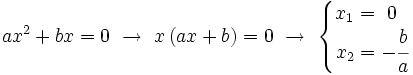
En la escena, pulsa "INICIO" para ver otros ejemplos.
En la escena, pulsa "INICIO" para ver otros ejemplos.
Ecuaciones de segundo grado sin termino lineal (caso b=0). Ejemplos.
Ecuaciones de segundo grado sin termino independiente (caso c=0). Ejemplos.
Ecuaciones de segundo grado incompletas (caso b=0)
Ecuaciones de segundo grado incompletas (caso c=0)
Ecuaciones de segundo grado incompletas (caso b=0):
Resuelve: 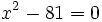
Resuelve: 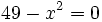
Resuelve: 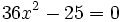
Resuelve: 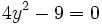
Ecuaciones de segundo grado incompletas (caso c=0):
Resuelve: 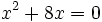
Resuelve: 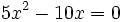
Resuelve: 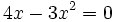
Actividades en la que aprenderás a resolver ecuaciones de segundo grado incompletas del tipo b=0.
Actividades en la que aprenderás a resolver ecuaciones de segundo grado incompletas del tipo c=0.
Ejercicios de autoevaluación sobre ecuaciones de segundo grado incompletas.
Ejercicios resueltos sobre ecuaciones de segundo grado incompletas.
Ejercicios propuestos
|
Ejercicios propuestos: Ecuaciones de segundo grado incompletas |
Factorización de polinomios de segundo grado
Factorización de polinomios de segundo grado. Ejemplos.
Factoriza:
a) 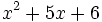
b) 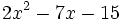
c) 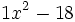
d) 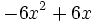
Reglas para resolver ecuaciones de segundo grado
Procedimiento
Para resolver una ecuación de segundo grado sigue los siguiente pasos:
- Lo primero que hay que hacer es ponerla en forma general. Para ello será necesario quitar denominadores, quitar paréntesis, simplificar, transponer y ordenar los términos.
- Una vez en forma general, si la ecuación es incompleta aplicaremos las técnicas explicadas para tal caso. Si la ecuación es completa usaremos la fórmula general.
- Una vez resuelta, opcionalmente podemos comprobar las soluciones, sustituyendo en la ecuación de partida.
Ejercicios resueltos:
Resuelve las siguientes ecuaciones:
- 1.
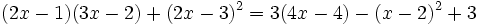
- 2.
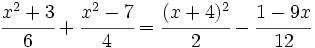
- 3.
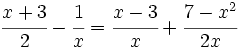
Soluciónes:
- 1.
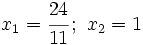 .
.
- 2.
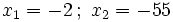 .
.
- 3.
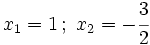 .
.
Tutorial en el que se explica la resolución de ecuaciones de 2º grado en donde no merece la pena utilizar la fórmula general de resolución.
Resuelve:
a) 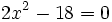
b) 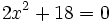
c) 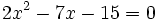
d) 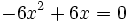
e) 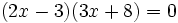
Resuelve: 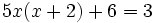
Resuelve: 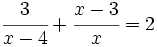
Ejercicios propuestos
|
Ejercicios propuestos: Resolución de problemas mediante ecuaciones de segundo grado |
Resolución de problemas mediante ecuaciones de segundo grado
Ejercicios resueltos:
- En un triángulo rectángulo, un cateto mide 2 cm menos que la hipotenusa y 14 cm más que el otro cateto. Calcular la longitud de los tres lados.
- Con 14 m de listones puedo colocar un rodapié a lo largo de toda una habitación rectangular, sin que sobre nada. ¿Qué dimensiones tiene la habitación sabiendo que su superficie es de 12 m2?
Solución 1: 10 cm, 24 cm y 26 cm.
Solución 2: 4 m y 3 m.- Si sumamos el cuadrado de un número más el cuádruplo del siguiente resulta 255. ¿De qué número se trata?
- Averigua el número que cumple la siguiente condición: si se multiplica su siguiente por el número disminuido en 3 unidades se obtiene 77.
- Mi padre tiene una finca rectangular que tiene 70 m de perímetro y 300 m2 de área. ¿Cuáles son las dimensiones de la finca?
En un rectángulo el largo mide (x+7) y el ancho (x+2). Si el área vale 36, halla el valor de x.
En un triángulo rectángulo un cateto excede al otro en 3 cm. Determina el perímetro del triángulo sabiendo que su área es 54 cm2.
En un triángulo rectángulo los catetos son dos números enteros pares consecutivos. Determina la hipotenusa del triángulo sabiendo que su área es 24 cm2.
Una piscina rectangular de 1 m de largo por 9 m de ancho está rodeada por un camino de ancho uniforme. Si el área del camino es 81 m2, ¿cuánto mide de ancho?
La altura de un triángulo es de 4 cm menos que el largo de su base. Si su área es de 30 cm2, ¿cuánto mide la altura y la base?
El volumen de una caja es de 405 unidades cúbicas. El largo de la caja es de "x" unidades, el ancho de "x+4" unidades y la altura de 9 unidades. Halla las dimensiones de la caja.
Ejercicios propuestos
|
Ejercicios propuestos: Resolución de problemas mediante ecuaciones de segundo grado |
Actividades y videotutoriales
Plantilla:Actividades y videotutoriales: ecuación de segundo grado