Plantilla:Dominio e imagen de una función (Bachiller)
De Wikipedia
| Revisión de 08:03 12 jun 2017 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) ← Ir a diferencia anterior |
Revisión de 08:30 12 jun 2017 Coordinador (Discusión | contribuciones) (→Simetrías de una función) Ir a siguiente diferencia → |
||
| Línea 157: | Línea 157: | ||
| ==Simetrías de una función== | ==Simetrías de una función== | ||
| + | {{Caja_Amarilla|texto=*Una función es '''par''' si cumple que: <math>f(x)=f(-x) \ , \forall \, x \in Dom_f</math>. En tal caso la gráfica es simétrica respecto del eje Y. | ||
| + | *Una función es '''impar''' si cumple que: <math>f(x)=-f(-x) \ , \forall \, x \in Dom_f</math>. En tal caso la gráfica es simétrica respecto del origen. | ||
| + | }} | ||
| + | {{p}} | ||
| {{Videotutoriales|titulo=Simetrías de una función|enunciado= | {{Videotutoriales|titulo=Simetrías de una función|enunciado= | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| Línea 178: | Línea 182: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
| {{ejercicio | {{ejercicio | ||
Revisión de 08:30 12 jun 2017
- Al conjunto de los valores que puede tomar la variable independiente
 , se le llama dominio de definición de la función. Lo representaremos por
, se le llama dominio de definición de la función. Lo representaremos por 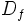 ó
ó 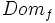
- La imagen, rango o recorrido de una función es el conjunto de valores que puede tomar la variable dependiente
 . Lo representaremos por
. Lo representaremos por 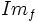 o
o 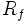 .
.
En esta escena podrás visualizar el dominio y la imagen de una función. Podrás elegir entre un tramo de recta (función lineal) o de parábola (función cuadrática).
El "dominio de definición" de la función "f" se denota Domf, y es el conjunto que forman los números reales "x" que tienen imagen segun "f"; o sea, los "x" tales que al calcular "f(x)" no se viola ninguna Regla Sagrada. A la hora de representar la gráfica de "f" lo primero SIEMPRE es determinar Domf, pues así sabremos en qué puntos del eje de abcisas hay curva y en qué puntos no la hay.
Razones para restringir el dominio de una función:
- Imposibilidad de realizar alguna operación con ciertos valores de
 que incumplan las quie hemos llamdo "reglas sagradas" del Cálculo. (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos, logaritmos de valores no positivos).
que incumplan las quie hemos llamdo "reglas sagradas" del Cálculo. (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos, logaritmos de valores no positivos).
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos).
- Por voluntad de quien propone la función.
Ejemplo: Dominio de definición de una función
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
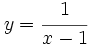
- b)
- c)
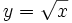
- c)
- d)
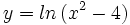
- d)
- e)
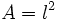 (Área de un cuadrado de lado
(Área de un cuadrado de lado 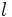 )
)
- e)
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png) , por voluntad del que ha definido la función, ya que, en principio, cualquier valor de
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
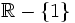 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
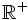 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
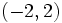 , porque el logaritmo de un número sólo existe si éste es positivo. Al resolver la inecuación
, porque el logaritmo de un número sólo existe si éste es positivo. Al resolver la inecuación 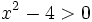 resulta que
resulta que 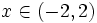 .
.
- d) Su dominio es
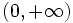 , porque el lado de un cuadrado sólo puede tomar valores positivos
, porque el lado de un cuadrado sólo puede tomar valores positivos
5 ejemplos.
Varios ejemplos.
15 ejemplos.
16 ejemplos.
10 ejemplos.
11 ejemplos.
7 ejemplos.
8 ejemplos.
4 ejemplos.
6 ejemplos.
7 ejemplos.
7 ejemplos.
Expresa el área de un círculo en función de la longitud de su circunferencia e indica su dominio y recorrido.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones polinómicas.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con quebrados algebraicos.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con radicales.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula y en este caso interviene el valor absoluto de funciones y cuando aparecen mezcladas funciones polinómicas, con quebrados y radicales.
Simetrías de una función
- Una función es par si cumple que:
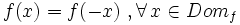 . En tal caso la gráfica es simétrica respecto del eje Y.
. En tal caso la gráfica es simétrica respecto del eje Y.
- Una función es impar si cumple que:
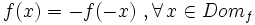 . En tal caso la gráfica es simétrica respecto del origen.
. En tal caso la gráfica es simétrica respecto del origen.
- La función "f" se dice "par" si f(-x) = f(x), y se dice "impar" si f(-x) = -f(x).
- Si "f" es par, su gráfica es simétrica respecto al eje de ordenadas.
- Si "f" es impar, su gráfica es simétrica respecto al origen de coordenadas.
- Obvio: si Dom f. no es simétrico respecto al punto "0", la función "f" no es par ni impar.
Ejemplos de funciones pares e impares. Interpretación gráfica.
Ejercicios propuestos
|
Ejercicios propuestos: Concepto de función y de dominio de una función |

