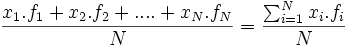Parámetros estadísticos
De Wikipedia
| Revisión de 16:41 20 jun 2007 Juanmf (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:48 20 jun 2007 Juanmf (Discusión | contribuciones) (→Media aritmética) Ir a siguiente diferencia → |
||
| Línea 24: | Línea 24: | ||
| <math> \bar x\ </math> = <math>\frac{x_1 + x_2 + ....+x_N} {N}={\sum_{i=1}^N x_i \over N} </math> donde N = nº total de individuos= <math>\sum_{i=1}^N f_i</math> | <math> \bar x\ </math> = <math>\frac{x_1 + x_2 + ....+x_N} {N}={\sum_{i=1}^N x_i \over N} </math> donde N = nº total de individuos= <math>\sum_{i=1}^N f_i</math> | ||
| </center> | </center> | ||
| + | Sin embargo, podemos observar que aparecen datos repetidos y que en un estudio estadístico tenemos los datos agrupados en una tabla en la que aparecen las frecuencias. Por tanto, podemos simplificar el cálculo de la media aritmética con la fórmula: | ||
| + | <center> | ||
| + | <math> \bar x\ </math> = <math>\frac{x_1.f_1 + x_2.f_2 + ....+x_N.f_N} {N}={\sum_{i=1}^N x_i.f_i \over N} </math> | ||
| + | </center> | ||
| + | Si la variable es continua, el cálculo se hace de la misma forma pero utilizando como <math> x_i</math> '''las marcas de clase''': los valores centrales de cada intervalo o la media aritmética de los extremos de cada intervalo. | ||
Revisión de 16:48 20 jun 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Después de haber representado los datos gráficamente, ahora llega el momento de hacer un estudio de los mismos. Si estamos estudiando la estatura de todos los alumnos y alumnas del instituto y necesitamos dar información de este estudio, parece lógico dar un dato que conocemos todos como media y que representa la estatura de todo el alumnado estudiado. Además de este dato existen otros datos (que llamaremos parámetros) que van a representar a toda la población o que nos van a informar sobre la población.
Parámetros estadísticos. Son datos que resumen el estudio realizado en la población. Pueden ser de dos tipos:
- Parámetros de centralización. Son datos que representan de forma global a toda la población. Entre ellos vamos a estudiar la media aritmética, la moda y la mediana.
- Parámetros de dispersión. Son datos que informan de la concentración o dispersión de los datos respecto de los parámetros de centralización. Por ejemplo el recorrido, la varianza y la desviación típica.
Parámetros de Centralización
Media aritmética
Se define la media aritmética como la suma de todos los datos dividida por el número de datos. Se representa por 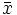 .
.
Para calcular la media aritmética hacemos:
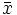 =
= 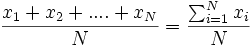 donde N = nº total de individuos=
donde N = nº total de individuos= 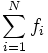
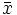 =
=