Relaciones de proporcionalidad entre magnitudes (1º ESO)
De Wikipedia
| Revisión de 09:46 13 ago 2017 Coordinador (Discusión | contribuciones) (→Razón y proporción) ← Ir a diferencia anterior |
Revisión de 09:47 13 ago 2017 Coordinador (Discusión | contribuciones) (→Razón y proporción) Ir a siguiente diferencia → |
||
| Línea 75: | Línea 75: | ||
| |titulo1=Autoevaluación: ''Cuarto proporcional'' | |titulo1=Autoevaluación: ''Cuarto proporcional'' | ||
| |descripcion=Ejercicios de autoevaluación sobre cuartos proporcionales. | |descripcion=Ejercicios de autoevaluación sobre cuartos proporcionales. | ||
| - | |url1=http://www.vitutor.com/di/p/a_3.html | + | |url1=http://www.vitutor.com/di/p/a_3e.html |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 09:47 13 ago 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
Un toque divertido para empezar el tema:
La aventura más Manga de Troncho y Poncho (a lo japonés). Es como si los Pokemon explicasen las magnitudes directa e inversamente proporcionales.
Puedes encontrar ejercicios sobre este vídeo y material similar en: http://www.angelitoons.com/
Razón y proporción
Tutorial en el que se explica y trabaja la proporción numérica, la razón de proporción, y cuando cuatro números guardan proporción. -
- 00:00 a 02:40: Introducción (ejemplos).
- 02:40 a 03:15: Definición de razón de proporción entre dos cantidades (números).
- 03:15 a 05:24: Ejemplos 1-2-3 de razón de proporción entre dos números.
- 05:24 a 08:15: Ejemplo 4 de aplicación de razón.
- 08:15 a 09:40: Definición de cuándo cuatro números guardan proporción. Producto de medios y producto de extremos. - 09:40 a 12:20: Ejemplos 5-6-7 de razón de proporción entre dos números. - 12:20 a Fin: Ejemplo 8 de aplicación de razón.
Estamos acostumbrados a dar información sobre situaciones de la vida cotidiana usando números. Hay ocasiones en las que un solo número no es suficiente y debemos compararlo con otra cantidad para poder comprender mejor la situación. Cuando comparamos dos cantidades formamos una razón.
Razón es el cociente entre dos números  y
y  . Se escribe
. Se escribe 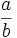 y se lee "
y se lee " es a
es a  ".
".
Una razón no tiene unidades y sirve para comparar, ya que indica el nº de veces que una cantidad es mayor que otra.
- En una primera escena te presentamos varios ejemplos de razón entre dos números para entender qué nos indica.
- En otra actividad te proponemos que halles la razón en tres casos concretos.
Una proporción es una igualdad entre dos razones: 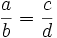 .
.
- En una primera escena te presentamos varios ejemplos de proporciones.
- En otra actividad te proponemos que compruebes si dos razones dadas forman o no una proporción.
Ejercicios de autoevaluación sobre proporciones.
Dado que el producto de medios es igual al de extremos, podemos calcular cualquier término de una proporción conociendo los otros tres.
Se llama cuarto proporcional al término que desconocemos en una proporción.
Actividades para aprender y practicar el cálculo del cuarto proporcional.
Ejercicios de autoevaluación sobre cuartos proporcionales.
(Pág. 152)
Relación de proporcionalidad directa
Dos magnitudes son directamente proporcionales cuando al multiplicar (resp. dividir) una de ellas por un número, la otra queda multiplicada (resp. dividida) por el mismo número.
La capacidad de un depósito de agua y el tiempo que tarda en llenarse son magnitudes directamente proporcionales, ya que si el depósito tiene el doble (o el triple,...) de capacidad, el tiempo que tarda en llenarse es el doble (o el triple,...).
Capacidad (litros) |
100 |
200 |
300 |
400 |
500 |
Tiempo (min) |
5 |
10 |
15 |
20 |
25 |
Actividades para aprender que son magnitudes directamente proporcionales.
Constante de proporcionalidad
Al dividir dos magnitudes directamente proporcionales siempre se obtiene el mismo valor. A dicho valor se le llama constante de proporcionalidad.
En el ejemplo anterior, en el que relacionabamos la capacidad de un depósito con el tiempo que tardaba en llenarse
Capacidad (litros) |
100 |
200 |
300 |
400 |
500 |
Tiempo (min) |
5 |
10 |
15 |
20 |
25 |
se observa que:
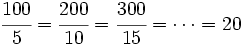
La constante de proporcinalidad es 20.
Actividades para aprender a calcular la constante de proporcionalidad directa.
(Pág. 153)
Relación de proporcionalidad inversa
Dos magnitudes son inversamente proporcionales cuando al multiplicar (resp. dividir) una de ellas por un número, la otra queda dividida (resp. multiplicada) por el mismo número.
El número de obreros que trabajan en una construcción y el tiempo que tardan en finalizarla son magnitudes inversamente proporcionales, ya que si el número de obreros es el doble (o el triple,...), el tiempo que tardan será la mitad (o la tercera parte, ...).
Número de obreros |
2 |
4 |
10 |
20 |
Tiempo que tardan (horas) |
20 |
10 |
4 |
2 |
Propiedad
Al multiplicar dos magnitudes inversamente proporcinales siempre se obtiene el mismo valor. A dicho valor se le denomina constante de proporcionalidad inversa.
En el ejemplo anterior, en el que relacionabamos el número de obreros y el tiempo que tardan en finalizar una obra
Número de obreros |
2 |
4 |
10 |
20 |
Tiempo que tardan (horas) |
20 |
10 |
4 |
2 |
se observa que:
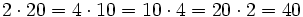
Actividades para que aprendas y practiques el cálculo de la constante de proporcionalidad inversa y sus uso para resolver problemas de proporcionalidad inversa.
Ejercicios
Ejercicios propuestos
|
Ejercicios propuestos: Relaciones de proporcionalidad entre magnitudes |

