Plantilla:Valor absoluto (1º Bach)
De Wikipedia
| Revisión de 08:37 16 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:52 22 sep 2017 Coordinador (Discusión | contribuciones) (→Inecuaciones con valor absoluto) Ir a siguiente diferencia → |
||
| Línea 133: | Línea 133: | ||
| :<math>\iff x \in \left ( -\infty , -3 \right ] \cup \left [ 3, +\infty \right ) \iff x \in \mathbb{R}-\left ( -3, 3 \right ) </math> | :<math>\iff x \in \left ( -\infty , -3 \right ] \cup \left [ 3, +\infty \right ) \iff x \in \mathbb{R}-\left ( -3, 3 \right ) </math> | ||
| - | b) <math>|x-2|\le 3 \iff -3<x-2<3 \iff -3+2<x-2+2<3+2 \iff</math> | + | b) <math>|x-2|\le 3 \iff -3 \le x-2 \le 3 \iff -3+2 \le x-2+2 \le 3+2 \iff</math> |
| - | :<math> \iff -1<x<5 \iff x \in \left [ -1 , 5 \right ]</math> | + | :<math> \iff -1 \le x \le 5 \iff x \in \left [ -1 , 5 \right ]</math> |
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Inecuaciones con valores absolutos}} | {{Inecuaciones con valores absolutos}} | ||
Revisión de 06:52 22 sep 2017
El valor absoluto o módulo de un número real  es el propio número
es el propio número  , si es positivo o nulo. Y su opuesto,
, si es positivo o nulo. Y su opuesto, 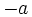 , si es negativo. Es decir:
, si es negativo. Es decir:
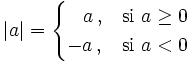
Desde un punto de vista geométrico, el valor absoluto de un número real  corresponde a la distancia a lo largo de la recta real desde
corresponde a la distancia a lo largo de la recta real desde  hasta el cero.
hasta el cero.
Propiedades del valor absoluto
Tutorial en el que se explica y trabaja el concepto matemático de valor absoluto de un número real y expresiones sencillas.
- 00:00 a 03:25: Definición matemática de valor absoluto y ejemplos iniciales.
- 03:25 a 11:10: Cálculo del valor absoluto de expresiones numéricas sencillas.
- 11:10 a 13:53: Propiedades del Valor Absoluto.
- Definición del valor absoluto de un número.
- Ejemplos.
- Propiedades del valor absoluto.
Como consecuencia, en una inecuación:
- Lo que está sumando en un lado de la desigualdad, pasa restando al otro miembro sin afectar a la desigualdad. Y viceversa.
- Lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa. En este caso la desigualdad sólo cambia de sentido si el número que pasa multiplicando o dividiendo es negativo.
¿Cuándo debe cambiar de sentido una desigualdad?. Ejemplos.
Ecuaciones con valor absoluto
Procedimiento
Para resolver ecuaciones con valor absoluto utilizaremos la 2ª de las propiedades del valor absoluto, que dice:
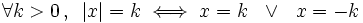
Resuelve:
a) 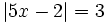
b) 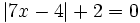
c) 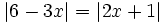
Resuelve:
a) 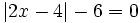
b) 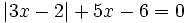
c) 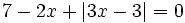
Resuelve:
Resuelve:
(pág. 33)
Inecuaciones con valor absoluto
Procedimiento
Para resolver inecuaciones con valor absoluto utilizaremos las propiedades 3ª y 4ª del valor absoluto, que dicen:
Ejercicios resueltos: Valor absoluto
¿Para qué valores de x se cumplen las siguientes desigualdades?
- a)
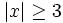
- b)
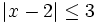
a) 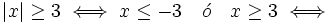
b) 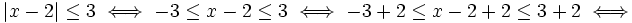
Inecuaciones con valor absoluto. Ejemplos.
Inecuaciones con valor absoluto. Ejemplos.
Resuelve:
- a)
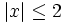
- b)
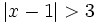
Resuelve: 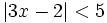
Resuelve: 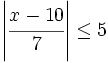
Resuelve: 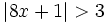
Resuelve: 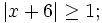
Resuelve: 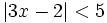
Resuelve:
a) 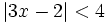
b) 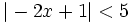
Resuelve: 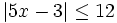
Resuelve: 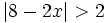
Resuelve: 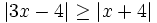
Resuelve: 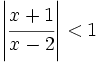
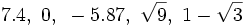
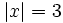
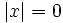
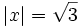
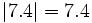
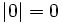
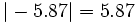
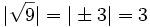
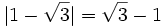
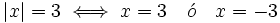
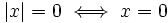
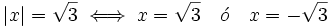
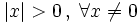
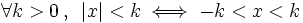
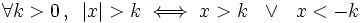
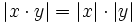
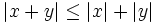
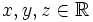 , se cumplen las siguientes propiedades:
, se cumplen las siguientes propiedades:
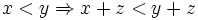
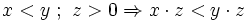
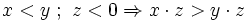
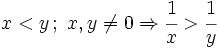
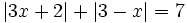
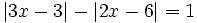
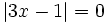
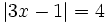
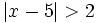
![\iff x \in \left ( -\infty , -3 \right ] \cup \left [ 3, +\infty \right ) \iff x \in \mathbb{R}-\left ( -3, 3 \right )](/wikipedia/images/math/7/8/c/78cd6dc5f9f2acad4c05dfc30174e0c9.png)
![\iff -1 \le x \le 5 \iff x \in \left [ -1 , 5 \right ]](/wikipedia/images/math/c/4/1/c41d22d69800fc9c4f7918de0410c4f4.png)

