Plantilla:Triángulos semejantes
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:26 17 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:29 17 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 20: | Línea 20: | ||
| ---- | ---- | ||
| (*) Dos elementos de dos figuras son '''homólogos''' si ocupan el mismo lugar en ambas figuras. | (*) Dos elementos de dos figuras son '''homólogos''' si ocupan el mismo lugar en ambas figuras. | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejemplo: Triángulos semejantes | ||
| - | |duracion=5'09" | ||
| - | |sinopsis=Ejemplo de semejanza de triángulos. | ||
| - | |url1=http://www.unicoos.com/clase/matematicas/2-eso/semejanza-y-teorema-de-thales/semejanza/semejanza-de-triangulos-01 | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 09:29 17 sep 2017
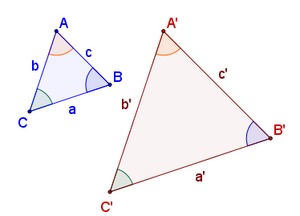
Se dice que dos figuras geométricas, y en particular dos triángulos, son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes.
Matemáticamente, la semejanza de triángulos la podemos expresar de la siguiente manera:
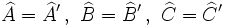
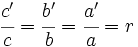
|
(*) Dos elementos de dos figuras son homólogos si ocupan el mismo lugar en ambas figuras.
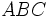
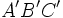
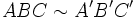
 se le llama razón de semejanza.
se le llama razón de semejanza.