Plantilla:Ángulos en un polígono de n lados
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:42 20 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:35 14 oct 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 15: | Línea 15: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Suma de los ángulos interiores de un polígono | ||
| + | |duracion=7´16" | ||
| + | |url1=https://www.youtube.com/watch?v=MbjzUC5p6lw | ||
| + | |sinopsis=*Suma de los ángulos interiores de un polígono cualquiera. | ||
| + | *Ejemplos de aplicación. | ||
| + | *Medida de los ángulos interiores de un polígono regular. | ||
| + | }} | ||
| {{Videotutoriales|titulo=Ángulos interiores de un polígono regular|enunciado= | {{Videotutoriales|titulo=Ángulos interiores de un polígono regular|enunciado= | ||
| {{Video_enlace_carreon | {{Video_enlace_carreon | ||
Revisión de 09:35 14 oct 2017
Propiedades
- La suma de los ángulos interiores de un polígono de
lados es igual a 
.
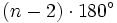- Si el polígono de lados es regular:
- Cada ángulo interior mide
.
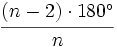- Cada ángulo exterior mide
.
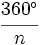- Cada ángulo interior mide
Demostración:
- Desde un vértice cualquiera del polígono se pueden trazar n-3 diagonales que dividen al polígono en n-2 triángulos. Sumando los ángulos de todos esos triángulos se obtiene la fórmula, ya que la suma de los ángulos de cada triángulo es 180º.
- Si además el polígono es regular:
- Al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n.
- Para ver la medida del ángulo exterior restaremos a 180º el ángulo interior:
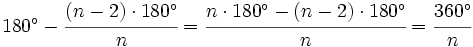
Suma de los ángulos interiores de un polígono (7´16") Sinopsis:- Suma de los ángulos interiores de un polígono cualquiera.
- Ejemplos de aplicación.
- Medida de los ángulos interiores de un polígono regular.
Tutorial 1 (9´02") Sinopsis: - Suma de los ángulos interiores de un triángulo.
- Cálculo de los ángulos interiores de un polígono regular y de sus suma.
Tutorial 2 (5´38") Sinopsis: Ángulos interiores de un cuadrado y de un hexágono regular.
Tutorial 3 (6´13") Sinopsis: Suma de los ángulos interiores de un polígono regular.
Tutorial 4 (3´24") Sinopsis: Deducción de la fórmula de la suma de los ángulos interiores de un polígono de n lados.
Ejercicio (2´20") Sinopsis:¿Existe un polígono convexo cuyos ángulos sumen 1440º? Indica su nombre y la cantidad de lados que tiene.
Ángulos exteriores de un polígono regular (1´28") Sinopsis: Ángulo exterior de un polígono regular
