Variables aleatorias
De Wikipedia
| Revisión de 14:03 1 jul 2007 Juanmf (Discusión | contribuciones) (→Definicion) ← Ir a diferencia anterior |
Revisión de 14:04 1 jul 2007 Juanmf (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | ==Definicion== | + | ==Definición== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Se llama '''''variable aleatoria''''' a toda aplicación | Se llama '''''variable aleatoria''''' a toda aplicación | ||
| Línea 58: | Línea 58: | ||
| ==Función de distribución== | ==Función de distribución== | ||
| - | + | {{Caja_Amarilla|texto= | |
| - | <br/> | + | |
| - | + | ||
| Dada una variable aleatoria | Dada una variable aleatoria | ||
| <math> | <math> | ||
| Línea 94: | Línea 92: | ||
| </math> | </math> | ||
| . | . | ||
| - | + | }} | |
| <br/> | <br/> | ||
Revisión de 14:04 1 jul 2007
Definición
Se llama variable aleatoria a toda aplicación
X
del espacio muestral
E
en un subconjunto de los numeros reales:
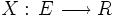
Al conjunto de valores de R asignados a los elementos de E se le llama recorrido de la variable aleatoria y se representa por
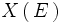 .
.
Una variable aleatoria es un valor numérico que corresponde al resultado de un
experimento aleatorio, como la suma de los puntos obtenidos al lanzar dos dados, el
número de lanzamientos de un dado hasta que aparece el cuatro, el número de personas que
suben en un determinado ascensor al mes, el tiempo de espera en la sala de un doctor...
Las variables aleatorias discretas son aquellas que pueden tomar solamente un
número finitio o un número infinito numerable de valores.
A este nivel, las unicas variables aleatorias que consideraremos son aquellas que toman
un número finito de valores. Un ejemplo de este tipo de variable aleatoria seria el
resultado de lanzar un dado.
Las variables aleatorias continuas son aquellas que pueden tomar cualquier
valor en un intervalo de la recta real. Un ejemplo de este tipo de variable aleatoria
seria la altura de una persona.
Función de distribución
Dada una variable aleatoria X , su función de distribución es la aplicación que a cada valor x de la variable le asigna la probabilidad de que ésta tome valores menores o iguales que x , y la denotamos por:
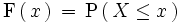
Como la función de distribución es una probabilidad,
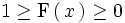 .
.

