Plantilla:Razón y proporción 1ºESO
De Wikipedia
| Revisión de 11:53 21 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:55 21 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 36: | Línea 36: | ||
| Quieres hacer una copia ampliada de una foto carné. Quieres que esa foto sea exactamente igual que la que ya tienes, pero más grande, es decir, que se respete la forma, pero no el tamaño. Lógicamente si duplicas el largo de la foto, estás obligado a duplicar el alto, ya que de lo contrario no se respetaría la forma original (saldría estirada o achatada). Matemáticamente, para que la nueva foto sea proporcional, la razón entre el largo de la ampliación y el largo de la original tiene que ser igual a la razón entre el ancho de la ampliación y el ancho de la original. Y eso es lo que dice la definición: proporción es igualdad de razones. | Quieres hacer una copia ampliada de una foto carné. Quieres que esa foto sea exactamente igual que la que ya tienes, pero más grande, es decir, que se respete la forma, pero no el tamaño. Lógicamente si duplicas el largo de la foto, estás obligado a duplicar el alto, ya que de lo contrario no se respetaría la forma original (saldría estirada o achatada). Matemáticamente, para que la nueva foto sea proporcional, la razón entre el largo de la ampliación y el largo de la original tiene que ser igual a la razón entre el ancho de la ampliación y el ancho de la original. Y eso es lo que dice la definición: proporción es igualdad de razones. | ||
| - | [[Imagen:proporcion.gif|center]] | + | <center>[[Imagen:proporcion.gif]][[Imagen:desproporcion.gif]]</center> |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:55 21 nov 2017
Tutorial en el que se explica y trabaja la proporción numérica, la razón de proporción, y cuando cuatro números guardan proporción. -
- 00:00 a 02:40: Introducción (ejemplos).
- 02:40 a 03:15: Definición de razón de proporción entre dos cantidades (números).
- 03:15 a 05:24: Ejemplos 1-2-3 de razón de proporción entre dos números.
- 05:24 a 08:15: Ejemplo 4 de aplicación de razón.
- 08:15 a 09:40: Definición de cuándo cuatro números guardan proporción. Producto de medios y producto de extremos. - 09:40 a 12:20: Ejemplos 5-6-7 de razón de proporción entre dos números. - 12:20 a Fin: Ejemplo 8 de aplicación de razón.
Estamos acostumbrados a dar información sobre situaciones de la vida cotidiana usando números. Hay ocasiones en las que un solo número no es suficiente y debemos compararlo con otra cantidad para poder comprender mejor la situación. Cuando comparamos dos cantidades formamos una razón.
Razón es el cociente entre dos números  y
y  . Se escribe
. Se escribe 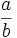 y se lee "
y se lee " es a
es a  ".
".
- Toda fracción puede ser considerada como una razón, pero no toda razón es una fracción, ya que una fracción es el cociente de dos números enteros, pero en una razón los números no tienen que ser necesariamente enteros.
- Cuando digamos "razón de a y b" nos referiremos habitualmente al cociente a/b, pero según el contexto, podremos considerar a/b o b/a, indistintamente.
- Podemos expresar una razón como número decimal o, cuando sea posible, como fracción.
- Una razón no tiene unidades y sirve para comparar, ya que indica el nº de veces que una cantidad es mayor que otra.
- En una primera escena te presentamos varios ejemplos de razón entre dos números para entender qué nos indica.
- En otra actividad te proponemos que halles la razón en tres casos concretos.
Una proporción es una igualdad entre dos razones: 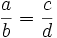 .
.
Para entender la definición anterior piensa en el siguiente ejemplo.
Quieres hacer una copia ampliada de una foto carné. Quieres que esa foto sea exactamente igual que la que ya tienes, pero más grande, es decir, que se respete la forma, pero no el tamaño. Lógicamente si duplicas el largo de la foto, estás obligado a duplicar el alto, ya que de lo contrario no se respetaría la forma original (saldría estirada o achatada). Matemáticamente, para que la nueva foto sea proporcional, la razón entre el largo de la ampliación y el largo de la original tiene que ser igual a la razón entre el ancho de la ampliación y el ancho de la original. Y eso es lo que dice la definición: proporción es igualdad de razones.
Conceptos de razón y proporción.
- En una primera escena te presentamos varios ejemplos de proporciones.
- En otra actividad te proponemos que compruebes si dos razones dadas forman o no una proporción.
Ejercicios de autoevaluación sobre proporciones.
Cálculo del cuarto proporcional
Se llama cuarto proporcional al término que desconocemos en una proporción.
Dado que si dos fracciones son equivalentes "el producto de medios es igual al de extremos", podemos calcular cualquier término de una proporción conociendo los otros tres.
Procedimiento
Para calcular el cuarto proporcional igualaremos el producto de extremos al producto de medios y despejaremos la incógnita:
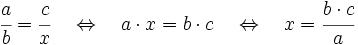
Actividades para aprender y practicar el cálculo del cuarto proporcional.
Actividades para aprender y practicar el cálculo del cuarto proporcional.
Actividades para aprender y practicar el cálculo del cuarto proporcional.
Ejercicios de autoevaluación sobre cuartos proporcionales.
Actividades
Completa la tabla sabiendo que la razones entre los elementos de las columnas son equivalentes.
En una clase de idiomas, la razón de niñas a niños es 5 a 8. Si hay 65 estudiantes, ¿cuántas niñas hay?
Majo tarda 3 horas en repartir 189 periódicos en su ruta. ¿Cuál es la razón por hora en la que entrega periódicos?
El servicio de limpieza Miranda cobra $2800 por limpiar 8 oficinas. ¿Cuál es el precio que cobra la compañía por limpiar una oficina?
Problema de comparación de tasas a partir de un tabla.
Distintos ejemplos de razón y proporcionalidad.
Aprende a completar tablas de razones equivalentes.
Problemas verbales de razones equivalentes (proporciones).
Comprender razones equivalentes (proporciones).
Razones equivalentes a partir de diagramas de barras.
Razones equivalentes y unidades de medida.
Razones parte:todo a partir de diagramas de barras.
Ejercicios:
- Calcula la razón de cada par de números y expresa el resultado como un número decimal.
- De las siguientes parejas de números, escoge aquellas que tengan razón 3/5.
- Calcula el término desconocido para cada proporción.



