Plantilla:Uso de letras en lugar de números
De Wikipedia
| Revisión de 11:05 22 nov 2017 Coordinador (Discusión | contribuciones) (→Cómo se traduce al lenguaje algebraico) ← Ir a diferencia anterior |
Revisión de 09:27 10 dic 2017 Coordinador (Discusión | contribuciones) (→Cómo se traduce al lenguaje algebraico) Ir a siguiente diferencia → |
||
| Línea 77: | Línea 77: | ||
| |sinopsis=Como se traducen expresiones del lenguaje cotidiano al lenguaje algebraico y su uso en el planteamiento de ecuaciones. | |sinopsis=Como se traducen expresiones del lenguaje cotidiano al lenguaje algebraico y su uso en el planteamiento de ecuaciones. | ||
| |url1=https://www.youtube.com/watch?v=BeNb5En9LeI&list=PLDjtbBXUusIxoU4YE4pbHYwXNFfVWexD7 | |url1=https://www.youtube.com/watch?v=BeNb5En9LeI&list=PLDjtbBXUusIxoU4YE4pbHYwXNFfVWexD7 | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejemplos 1 | ||
| + | |duracion=3'43" | ||
| + | |sinopsis=Ejemplos de cómo escribir expresiones básicas con variables. | ||
| + | |url1=https://www.youtube.com/watch?v=Wfb7ILDo_iw | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejemplos 2 | ||
| + | |duracion=1'39" | ||
| + | |sinopsis=Ejemplos de cómo escribir expresiones con variables. | ||
| + | |url1=https://www.youtube.com/watch?v=8qwW0PCRLLc | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejemplos 3 | ||
| + | |duracion=2'47" | ||
| + | |sinopsis=Ejemplos de cómo escribir expresiones con variables y paréntesis. | ||
| + | |url1=https://www.youtube.com/watch?v=PmXo8O1-BMw | ||
| }} | }} | ||
| ---- | ---- | ||
| Línea 286: | Línea 305: | ||
| }} | }} | ||
| {{Actividades|titulo=Traducir al lenguaje algebraico|enunciado= | {{Actividades|titulo=Traducir al lenguaje algebraico|enunciado= | ||
| - | {{AI_anaya|titulo1=Actividad 1 | + | {{AI_anaya|titulo1=Actividad 1a |
| |descripcion=Aprende a manejar expresiones algebraicas | |descripcion=Aprende a manejar expresiones algebraicas | ||
| |url1=http://web.educastur.princast.es/ies/pravia/carpetas/recursos/mates/anaya1/datos/10/01.htm | |url1=http://web.educastur.princast.es/ies/pravia/carpetas/recursos/mates/anaya1/datos/10/01.htm | ||
| }} | }} | ||
| - | {{AI_anaya|titulo1=Actividad 2 | + | {{AI_anaya|titulo1=Actividad 1b |
| |descripcion= | |descripcion= | ||
| Línea 304: | Línea 323: | ||
| }} | }} | ||
| {{AI_cidead | {{AI_cidead | ||
| - | |titulo1=Actividad 3 | + | |titulo1=Actividad 2a |
| |descripcion=Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico. | |descripcion=Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena7/1quincena7_contenidos_1b.htm | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena7/1quincena7_contenidos_1b.htm | ||
| }} | }} | ||
| {{AI_cidead | {{AI_cidead | ||
| - | |titulo1=Actividad 4 | + | |titulo1=Actividad 2b |
| + | |descripcion=Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena7/1quincena7_contenidos_1b.htm | ||
| + | }} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Actividad 2c | ||
| |descripcion=Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico. | |descripcion=Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_contenidos_1b.htm | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_contenidos_1b.htm | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 3a | ||
| + | |descripcion=Cómo escribir expresiones básicas con variables. | ||
| + | |url1=https://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-writing-expressionss/a/writing-basic-algebraic-expressions | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 3b | ||
| + | |descripcion=Cómo escribir expresiones con variables. | ||
| + | |url1=https://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-writing-expressionss/a/writing-expressions-with-variables | ||
| }} | }} | ||
| ---- | ---- | ||
Revisión de 09:27 10 dic 2017
Muchas veces, las Matemáticas requieren trabajar con números cuyo valor es desconocido o variable. En tales casos, los números se representan mediante letras y se operan con ellas utilizando las mismas reglas que cuando trabajamos con números. Estamos traduciendo al "lenguaje de las Matemáticas".
Llamaremos lenguaje algebraico al conjunto de símbolos (números, letras, símbolos de operación) y reglas que se utilizan para la transmisión de ideas matemáticas. De su estudio se encarga la parte de las matemáticas denominada álgebra.
Cómo se traduce al lenguaje algebraico
Al pasar del lenguaje convencional al lenguaje algebraico, debemos tener en cuenta algunas cosas:
- Los elementos desconocidos o aquellos que no tienen un valor fijo (variables) se representan mediante letras, mientras que aquellos que tienen su valor completamente determinado (constantes) se expresan con números.
- Si un enunciado habla de dos números que pueden ser diferentes, es necesario usar una letra distinta para cada uno. Cuando una letra aparece repetida en un mismo enunciado, se entiende que son varias referencias a un mismo número.
- Las relaciones entre números y variables se expresan mediante operaciones matemáticas.
Veamos algunas situaciones en la que resulta conveniente recurrir al lenguaje algebraico:
- Expresión de propiedades o reglas
Por ejemplo, la propiedad conmutativa del producto de dos números dice que "el orden de los factores no altera el producto". Ésto lo podemos expresar usando letras, de la siguiente manera:
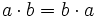
La regla de la división dice que "el dividendo es igual al divisor por el cociente más el resto". Ésto lo podemos expresar usando letras, de la siguiente manera:
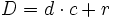
- Expresión de fórmulas
Por ejemplo, la fórmula del área del triángulo dice que "el área de un triángulo es igual a la base por la altura partido por 2", que podemos expresar con letras:
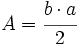
- Generalización de relaciones numéricas
Si consideramos la siguiente sucesión numérica
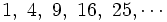
la expresión 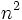 sirve para generalizar sus términos, de manera que, si yo quiero obtener el término que ocupa el séptimo lugar, tan solo tendré que sustituir la letra
sirve para generalizar sus términos, de manera que, si yo quiero obtener el término que ocupa el séptimo lugar, tan solo tendré que sustituir la letra  por el número 7,
por el número 7,
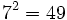
- Expresión de números desconocidos y planteamiento de ecuaciones
Por ejemplo, "la suma de dos números consecutivos es igual a 21" lo podemos expresar
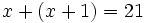
donde estamos utilizando la letra  para representar al primer número y la expresión
para representar al primer número y la expresión 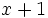 para representar al segundo número.
para representar al segundo número.
Ejercicio resuelto: Traducir al lenguaje algebraico
Traduce al lenguaje algebraico las siguientes expresiones del lenguaje habitual:
- a) El doble de un número menos cuatro unidades.
- b) La mitad de sumarle 5 al triple de un número.
- c) El perímetro y el área de un terreno rectangular.
a) Si llamamos  al número, entonces el doble del número menos cuatro unidades es
al número, entonces el doble del número menos cuatro unidades es 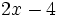 .
.
b) Llamando  al número, la mitad de sumarle 5 al triple de dicho número es
al número, la mitad de sumarle 5 al triple de dicho número es 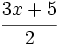
c) Si suponemos que el terreno rectangular mide  de largo e
de largo e  de ancho, tenemos:
de ancho, tenemos:
- Perimetro:
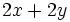
- Area:
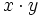
Paso de lenguaje habitual a lenguaje algebraico y viceversa.
Vamos a ver la diferencia entre el lenguaje aritmético y el lenguaje algebraico
Como se traducen expresiones del lenguaje cotidiano al lenguaje algebraico y su uso en el planteamiento de ecuaciones.
Como se traducen expresiones del lenguaje cotidiano al lenguaje algebraico.
Como se traducen expresiones del lenguaje cotidiano al lenguaje algebraico.
Letras en lugar de números. El lenguaje algebraico es la base que te permitirá plantear ecuaciones para resolver problemas.
Como se traducen expresiones del lenguaje cotidiano al lenguaje algebraico y su uso en el planteamiento de ecuaciones.
Ejemplos de cómo escribir expresiones básicas con variables.
Ejemplos de cómo escribir expresiones con variables.
Ejemplos de cómo escribir expresiones con variables y paréntesis.
Escribe en lenguaje algebraico:
Pablo tenía "x" dólares, cobró "m" dólares y le regalaron "z" dólares.¿Cuánto tiene Pablo?Escribe en lenguaje algebraico:
Se compraron (m-1) vacas por 2000 dólares.¿Cuál es el precio de cada vaca?Escribe en lenguaje algebraico:
Compré "n" sombreros por "x" dólares. ¿A cómo habría salido cada sombrero si hubiera comprado 2 sombreros menos por el mismo precio?Escribe en lenguaje algebraico:
Tenía "x" dólares y me pagaron "n". Si el dinero que tengo lo empleo todo en comprar (m-1) libros, ¿a cómo sale cada libro?Escribe en lenguaje algebraico:
José tiene "n" dólares; Juan tiene la tercera parte de la de José; Ana la cuarta parte del duplo de lo de José. la suma de lo que tienen los tres es menor que 3000 dólares. ¿Cuánto falta a esta suma para ser igual a 3000 dólares?Escribe en lenguaje algebraico:
La suma de tres números pares consecutivos es igual al triple del menor, más las tres cuartas partes del mayor.Escribe en lenguaje algebraico:
¿Cuál es el largo de un rectángulo, si se sabe que el largo es tres veces su ancho?Escribe en lenguaje algebraico:
El doble de un número equivale al triple de su antecesor excedido en siete.Escribe en lenguaje algebraico:
El cuadrado de la suma de dos números es igual a 49.Escribe en lenguaje algebraico:
Las dos terceras partes de un número, más el triple de su consecutivo, menos su recíproco equivale a 10.Escribe en lenguaje algebraico:
La mitad de un número más el cuadrado del mismo.Escribe en lenguaje algebraico:
Un número más seis, menos 15, es igual al cuadrado de otro número.Escribe en lenguaje algebraico:
La octava parte de un número es igual a un tercio de la suma de otros dos.Escribe un enunciado para la siguiente expresión algebraica: 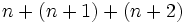
Escribe un enunciado para la siguiente expresión algebraica: 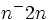
Expresa en lenguaje algebraico:
- 1) El doble de x.
- 2) El triple de y.
- 3) El doble de x más el triple de y.
- 4) El triple de x más el cuadrado de y.
- 5) La suma de x e y es 10.
- 6) El producto de x y de y es 24.
- 7) El cuadrado de x es 16.
- 8) El doble de x menos 5 es igual a 17.
- 9) El valor de x kg de naranjas a 2 euros el kilo.
- 10) El valor de y kg de mandarinas a 3 euros el kilo.
- 11) El valor de x kg de naranjas a 2 euros el kilo más y kg de mandarinas a 3 euros el kilo.
- 12) El valor de a metros de cinta a 1 euro el metro.
- 13) Cinco multiplicado por n más tres.
- 14) Seis multiplicado por ocho, menos n.
- 15) El doble de x, más uno, es quince.
Expresa en lenguaje algebraico:
- 16) El triple de x, menos uno, es veintiseis.
- 17) El cuadrado de x es igual a su doble.
- 18) El cubo de x es igual a su triple.
- 19) Cuatro multiplicado por la suma de x más y es igual a setenta y dos.
- 20) El triple de x, menos ocho, es igual a diez.
- 21) El número x es tres unidades mayor que y.
- 22) El número x es 3 unidades menor que el número y.
- 23) El doble de x es 5 veces el número y.
- 24) El número x es el doble del número y.
- 25) El triple de x es igual al doble de y.
- 26) El doble de a menos uno es igual al número b.
- 27) x es múltiplo de y.
- 28) El cuadrado de un número es igual a 225.
- 29) El cubo de un número es igual a 27.
- 30) La mitad de un número más la quinta parte del mismo número.
- 31) El cuadrado de un número más el cubo del mismo número.
- 32) El triple de x más el cuadrado de y más 5.
- 33) La mitad de la edad de Luis.
- 33) La mitad de la edad de Luis es 8.
- 35) El cuadrado de x es menor que 26.
- 36) La suma del cuadrado de un número y 30 es 46.
Sean "x", "y" y "z" números enteros:
- 37) Expresa con ellos la propiedad conmutativa de la suma.
- 38) Expresa con ellos la propiedad conmutativa del producto.
- 39) Expresa con ellos la propiedad asociativa de la suma.
- 40) Expresa con ellos la propiedad asociativa del producto.
- 41) Expresa con ellos la propiedad distributiva del producto respecto de la suma.
- 42) Expresa con ellos la propiedad distributiva del producto respecto de la resta.
- 43) Expresa el cuadrado de x más el cuadrado de y más el cuadrado de z.
Traduce al lenguaje algebraico los siguientes enunciados:
- a) Número de ruedas necesarias para fabricar x coches.
- b) Número de céntimos necesarios para cambiar por x euros.
- c) Número de patas que hay en un corral con a gallinas y b patos.
- d) Número de personas que hay en una habitación después de llegar 2.
- e) Número de cromos que me quedan después de perder 2 en un juego.
- f) La edad de un padre es triple que la del hijo.
- g) Un número más 3 unidades.
- h) Un número menos 7 unidades.
- i) La mitad de un número.
- j) El doble de un número menos 3 unidades.
- k) Restar la mitad de un número a 2.
- l) Añadir 8 al doble de un número.
- m) El doble de un número menos su mitad.
- n) Dos números pares consecutivos.
- o) Dos ángulos de un triángulo que se diferencian en 20º.
- p) La tercera parte de un número más su quinta parte.
- q) Número de personas casadas después de celebrarse x matrimonios.
- r) Dos quintos de un número.
- s) El triple de un número más 1.
- t) Un ciclista ha recorrido 87 km, ¿cuánto le queda para la meta?
- u) La edad de Pedro hace 4 años.
- v) La edad de Juan dentro de 15 años.
- w) La cuarta parte de una cantidad de dinero más 50.
- x) Restar a la quinta parte de un número 4 unidades.
- y) Dos números de diferencian en 5 unidades.
- z) Mi padre me da el doble de dinero que tenía. ¿Cuánto tengo ahora?
- a') Dos números impares consecutivos.
- b') Distancia recorrida por un coche en 6 horas.
Aprende a manejar expresiones algebraicas
Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico.
Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico.
Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico.
Cómo escribir expresiones básicas con variables.
Cómo escribir expresiones con variables.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.

