Ejercicios: Números complejos (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 13:12 21 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 28: | Línea 28: | ||
| |url1=https://www.youtube.com/watch?v=1B6VmZxkaZk | |url1=https://www.youtube.com/watch?v=1B6VmZxkaZk | ||
| |sinopsis=Números complejos en forma binómica: | |sinopsis=Números complejos en forma binómica: | ||
| - | *Parte real y parte imaginaria. | + | *'''Parte real y parte imaginaria de un número complejo'''. |
| - | *Complejos conjugados, iguales y opuestos. | + | *'''Complejos conjugados, iguales y opuestos.''' |
| - | **Ejercicio 1: Si el complejo ''a + 4i'' es conjugado con ''(2a - 1)+(3b + 2)i'', calcula ''a<sup>2</sup> + b<sup>2</sup>''. | + | **'''Ejercicio 1:''' Si el complejo ''a + 4i'' es conjugado con ''(2a - 1)+(3b + 2)i'', calcula ''a<sup>2</sup> + b<sup>2</sup>''. |
| - | **Ejercicio 2: ¿Cuál es el valor de ''a<sup>b</sup>'' si ''(a - 3) - (b - 2)i'' es opuesto a ''1 - (a - 1)i''. | + | **'''Ejercicio 2:''' ¿Cuál es el valor de ''a<sup>b</sup>'' si ''(a - 3) - (b - 2)i'' es opuesto a ''1 - (a - 1)i''. |
| - | *Suma, resta, producto, cociente de números complejos. | + | *'''Suma, resta, producto, cociente de números complejos.''' |
| - | **Ejercicio 3: Dados ''z<sub>1</sub> = 2 - 3i'' y ''z<sub>2</sub> = -1 - 2i'', calcula ''z<sub>1</sub> - ''z<sub>2</sub>''. | + | **'''Ejercicio 3:''' Dados ''z<sub>1</sub> = 2 - 3i'' y ''z<sub>2</sub> = -1 - 2i'', calcula ''z<sub>1</sub> - ''z<sub>2</sub>''. |
| - | **Ejercicio 4: Calcula ''(3 + 2i)·(5 + 3i)''. | + | **'''Ejercicio 4:''' Calcula ''(3 + 2i)·(5 + 3i)''. |
| - | **Ejercicio 5: Calcula ''(2 + 3i):(3 + i)''. | + | **'''Ejercicio 5:''' Calcula ''(2 + 3i):(3 + i)''. |
| - | **Ejercicio 6: Calcula el valor de ''k'' para que el cociente ''(9 - ki):(3k - i)'' sea: a) real; b) Imaginario puro. | + | **'''Ejercicio 6:''' Calcula el valor de ''k'' para que el cociente ''(9 - ki):(3k - i)'' sea: a) real; b) Imaginario puro. |
| - | *Módulo de un número complejo. | + | *'''Módulo de un número complejo.''' |
| - | **Ejercicio 7: Calcula ''<math>|(2 + 8i) + (1 - 4i)|\;</math>''. | + | **'''Ejercicio 7:''' Calcula ''<math>|(2 + 8i) + (1 - 4i)|\;</math>''. |
| - | **Ejercicio 8: Calcula ''<math>|(1 + i)^2 \cdot (1 - i)|</math>''. | + | **'''Ejercicio 8:''' Calcula ''<math>|(1 + i)^2 \cdot (1 - i)|</math>''. |
| - | *El plano complejo. | + | *'''El plano complejo.''' |
| - | *Forma polar y forma trigonométrica de un número complejo. Conversión entre polar y binómica. | + | *'''Forma polar y forma trigonométrica de un número complejo. Conversión entre polar y binómica.''' |
| - | **Ejercicio 9: Convierte a forma polar: a) <math>-1+\sqrt{3}i</math>;{{b4}} b) <math>3\;</math>;{{b4}} c) <math>5i\;</math> | + | **'''Ejercicio 9:''' Convierte a forma polar: a) <math>-1+\sqrt{3}i</math>;{{b4}} b) <math>3\;</math>;{{b4}} c) <math>5i\;</math> |
| - | **Ejercicio 10: Convierte a forma binómica: a) <math>2_{60^\circ}</math>;{{b4}} b) <math>10_{120^\circ}</math>;{{b4}} c) <math>1_{180^\circ}</math>;{{b4}} d) <math>1_{90^\circ}</math>. | + | **'''Ejercicio 10:''' Convierte a forma binómica: a) <math>2_{60^\circ}</math>;{{b4}} b) <math>10_{120^\circ}</math>;{{b4}} c) <math>1_{180^\circ}</math>;{{b4}} d) <math>1_{90^\circ}</math>. |
| - | **Ejercicio 11: Calcula el opuesto y el conjugado de <math>5_{150^\circ}</math>. | + | **'''Ejercicio 11:''' Calcula el opuesto y el conjugado de <math>5_{150^\circ}</math>. |
| - | *Producto, cociente, potencia y raíz en forma polar. Fórmula de Moivre. | + | *'''Producto, cociente, potencia y raíz en forma polar. Fórmula de Moivre.''' |
| - | **Ejercicio 12: Calcula <math>2_{30^\circ} \cdot 3_{15^\circ}</math>. | + | **'''Ejercicio 12:''' Calcula <math>2_{30^\circ} \cdot 3_{15^\circ}</math>. |
| - | **Ejercicio 13: Calcula <math>20_{45^\circ} : 4_{15^\circ}</math>. | + | **'''Ejercicio 13:''' Calcula <math>20_{45^\circ} : 4_{15^\circ}</math>. |
| - | **Ejercicio 14: Calcula <math>(2_{3^\circ})^{10}</math>. | + | **'''Ejercicio 14:''' Calcula <math>(2_{3^\circ})^{10}</math>. |
| - | **Ejercicio 15: Expresa en forma binómica usando la fórmula de Moivre: <math>(\sqrt{2}_{45^\circ})^{10}</math>. | + | **'''Ejercicio 15:''' Expresa en forma binómica usando la fórmula de Moivre: <math>(\sqrt{2}_{45^\circ})^{10}</math>. |
| - | **Ejercicio 16: Resuelve en el conjunto de los números complejos: <math>x^3=1\;</math>. | + | **'''Ejercicio 16:''' Resuelve en el conjunto de los números complejos: <math>x^3=1\;</math>. |
| }} | }} | ||
| [[Categoría: Ejercicios de Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | [[Categoría: Ejercicios de Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | ||
Revisión actual
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
|
Ejercicios de repaso |
Números complejos en forma binómica:
- Parte real y parte imaginaria de un número complejo.
- Complejos conjugados, iguales y opuestos.
- Ejercicio 1: Si el complejo a + 4i es conjugado con (2a - 1)+(3b + 2)i, calcula a2 + b2.
- Ejercicio 2: ¿Cuál es el valor de ab si (a - 3) - (b - 2)i es opuesto a 1 - (a - 1)i.
- Suma, resta, producto, cociente de números complejos.
- Ejercicio 3: Dados z1 = 2 - 3i y z2 = -1 - 2i, calcula z1 - z2.
- Ejercicio 4: Calcula (3 + 2i)·(5 + 3i).
- Ejercicio 5: Calcula (2 + 3i):(3 + i).
- Ejercicio 6: Calcula el valor de k para que el cociente (9 - ki):(3k - i) sea: a) real; b) Imaginario puro.
- Módulo de un número complejo.
- Ejercicio 7: Calcula
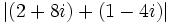 .
.
- Ejercicio 8: Calcula
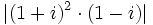 .
.
- Ejercicio 7: Calcula
- El plano complejo.
- Forma polar y forma trigonométrica de un número complejo. Conversión entre polar y binómica.
- Ejercicio 9: Convierte a forma polar: a)
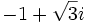 ; b)
; b) 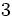 ; c)
; c) 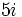
- Ejercicio 10: Convierte a forma binómica: a)
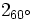 ; b)
; b) 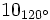 ; c)
; c) 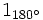 ; d)
; d) 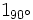 .
.
- Ejercicio 11: Calcula el opuesto y el conjugado de
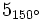 .
.
- Ejercicio 9: Convierte a forma polar: a)
- Producto, cociente, potencia y raíz en forma polar. Fórmula de Moivre.
- Ejercicio 12: Calcula
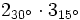 .
.
- Ejercicio 13: Calcula
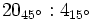 .
.
- Ejercicio 14: Calcula
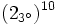 .
.
- Ejercicio 15: Expresa en forma binómica usando la fórmula de Moivre:
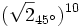 .
.
- Ejercicio 16: Resuelve en el conjunto de los números complejos:
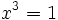 .
.
- Ejercicio 12: Calcula

