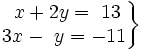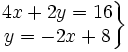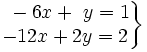Plantilla:Número de soluciones de un sistema
De Wikipedia
| Revisión de 10:08 28 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 104: | Línea 104: | ||
| |descripcion=Número de soluciones de un sistema de ecuaciones: método gráfico. | |descripcion=Número de soluciones de un sistema de ecuaciones: método gráfico. | ||
| |url1=http://es.khanacademy.org/math/algebra/systems-of-linear-equations/possible-number-of-solutions-of-systems-of-linear-equations/e/graphical-solutions-to-systems | |url1=http://es.khanacademy.org/math/algebra/systems-of-linear-equations/possible-number-of-solutions-of-systems-of-linear-equations/e/graphical-solutions-to-systems | ||
| - | }} | ||
| - | {{AI_Khan | ||
| - | |titulo1=Autoevaluación 1b | ||
| - | |descripcion=Número de soluciones de un sistema de ecuaciones: método algebraico. | ||
| - | |url1=http://es.khanacademy.org/math/algebra/systems-of-linear-equations/possible-number-of-solutions-of-systems-of-linear-equations/e/constructing-consistent-and-inconsistent-system | ||
| }} | }} | ||
| {{AI_vitutor | {{AI_vitutor | ||
Revisión actual
Discutir un sistema consiste en decir si el sistema tiene o no tiene solución, y caso de tener, si hay un número finito o infinito de soluciones.
- Un sistema es compatible si tiene solución e incompatible si no la tiene.
- Un sistema es determinado si tiene un número finito de soluciones e indeterminado si tiene infinitas soluciones.
Al discutir un sistema usaremos las siguientes siglas para abreviar:
- S.C.D. : Sistema Compatible Determinado (un número finito de soluciones)
- S.C.I. : Sistema Compatible Indeterminado (infinitas soluciones)
- S.I. : Sistema Incompatible (sin solución)
Discusión de sistemas lineales 2x2
Un sistema 2x2 de ecuaciones lineales puede ser:
- Compatible determinado (S.C.D.): 1 solución
- Compatible indeterminado (S.C.I.): Infinitas soluciones.
- Incompatible (S.I): 0 soluciones.
En efecto, razonando a partir de sus representaciones gráficas:
- Si las dos rectas se cortan en un punto: 1 solución (S.C.D.)
- Si las dos rectas son coincidentes: Infinitas soluciones (S.C.I.)
- Si las rectas son paralelas: 0 soluciones (S.I.)
Ejercicio 1 (5´30") Sinopsis: Averigua si el siguiente sistema es compatible (consistente) o incompatible (inconsistente):
Ejercicio 2 (5´12") Sinopsis: Averigua si el siguiente sistema es compatible determinado o compatible indeterminado:
Ejercicio 3 (3´27") Sinopsis: A partir de la gráfica del video identifica sistemas con o sin solución.
Ejercicio 4 (13´05") Sinopsis: Determina el número de soluciones del siguiente sistema:
Ejercicio 5 (9´28") Sinopsis: Determina el número de soluciones de los siguientes sistemas:
- a)
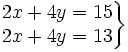
- b)
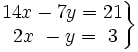
- c)
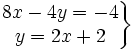
- d)
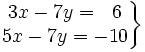
- e)
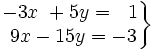
Ejercicio 6 (2´14") Sinopsis: ¿Cuántas soluciones tiene un sistema si tiene al menos dos?
Actividad 1 Descripción: Actividades en las que aprenderás a determinar el número de soluciones de un sistema de ecuaciones lineales con dos incógnitas y a interpretarlo gráficamente.
Actividad 2 Descripción: Actividades en las que aprenderás a determinar el número de soluciones de un sistema de ecuaciones lineales con dos incógnitas y a interpretarlo gráficamente.
Actividad 3a Descripción: En esta escena podrás interactuar para ver la representación gráfica de los distintos tipos de sistemas según el número de soluciones y contestar a algunas preguntas.
Actividad 3b Descripción: En esta escena podrás ver 3 ejemplos con los distintos tipos de sistemas según el número de soluciones y contestar a una serie preguntas en relación a ellos.
Autoevaluación 1a Descripción: Número de soluciones de un sistema de ecuaciones: método gráfico.
Autoevaluación 2 Descripción: Ejercicios de autoevaluación sobre los tipos de sistemas lineales dependiendo del número de soluciones.
