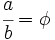Semejanza de rectángulos (4ºESO Académicas)
De Wikipedia
| Revisión de 08:15 5 feb 2019 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:19 5 feb 2019 Coordinador (Discusión | contribuciones) (→El rectángulo áureo) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| + | {{p}} | ||
| + | ==Rectángulos semejantes== | ||
| + | {{Teorema_sin_demo|titulo=Proposición|enunciado=Dos rectángulos son semejantes si sus dimensiones (largo y ancho) son proporcionales.}} | ||
| {{p}} | {{p}} | ||
| ==El rectángulo áureo== | ==El rectángulo áureo== | ||
| Línea 12: | Línea 15: | ||
| {{Construcción del rectángulo áureo}} | {{Construcción del rectángulo áureo}} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
| {{ejercicio | {{ejercicio | ||
Revisión de 08:19 5 feb 2019
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Rectángulos semejantes
El rectángulo áureo
El rectángulo áureo (o rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual al número áureo. Los griegos consideraban que un rectángulo de tales características era especialmente armonioso. Esta proporción de medidas se ha utilizado con mucha frecuencia en el arte. Proposición 2
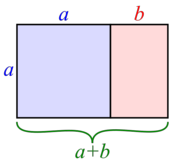
Demostración: Partimos de un rectángulo áureo. Lo dividimos en un cuadrado de lado su lado menor y otro rectángulo pequeño, como se observa en la Fig. 2. Veamos que el rectángulo pequeño también es un rectángulo áureo. Para ello tendremos que comprobar que Por ser el rectángulo de partida un rectángulo áureo, se cumple que la proporción entre sus lados es el número áureo: 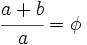 Operando:
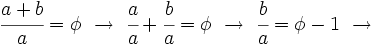 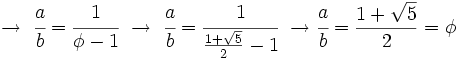 |
Construcción del rectángulo áureo
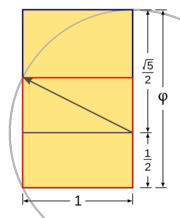
Construcción del rectángulo áureo con regla y compás
Demostración: Si te fijas en la Fig. 3, basta con demostrar que el segmento que se obtiene en el paso 2 mide 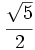 , para lo cual basta con usar el teorema de Pitágoras. , para lo cual basta con usar el teorema de Pitágoras.En la escena puedes ver la construcción del número de oro basada en una construcción gráfica que se encuentra en un libro de Euclides (siglo III a.C.).
Construcción con regla y compás de la sección áurea de un segmento y del rectángulo áureo. |
Ejercicios propuestos
|
Ejercicios propuestos: Semejanza de rectángulos |