Relaciones trigonométricas fundamentales (4ºESO Académicas)
De Wikipedia
| Revisión de 08:30 18 feb 2019 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:32 18 feb 2019 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) Ir a siguiente diferencia → |
||
| Línea 20: | Línea 20: | ||
| (Pág. 146) | (Pág. 146) | ||
| - | [[Imagen:yellow_star.png|12px]] 1, 2 | + | [[Imagen:red_star.png|12px]] 1, 2, 3, 4, 5 |
| }} | }} | ||
Revisión de 08:32 18 feb 2019
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Relaciones fundamentales de la trigonometría
Relaciones fundamentales de la trigonometría
1. 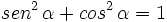 (Identidad pitagórica)
(Identidad pitagórica)
2. 
3. 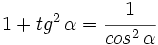
Demostración de las relaciones fundamentales de la trigonometría.
Demostración de la identidad pitagórica.
Dada una de las razones trigonométricas de un ángulo, determinar las cinco restantes, haciendo uso de las relaciones fundamentales de la trigonometría.
- a)
 ; b)
; b) 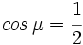 ; c)
; c) 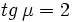
- d)
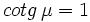 ; e)
; e) 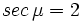 ; f)
; f) 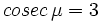
Simplifica: 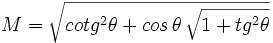
Comprueba las siguientes identidades trigonométricas:
a) 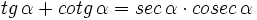
b) 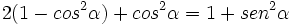
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Identidades trigonométricas. Ejercicios.
Identidades trigonométricas. Ejercicios.
Identidades trigonométricas. Ejercicios.
Ejercicio resuelto: Razones trigonométricas de un ángulo agudo
Sea
 un ángulo agudo.
un ángulo agudo.
- Sabiendo que
 , calcular
, calcular 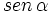 y
y 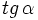 .
.
- Sabiendo que
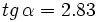 , calcular
, calcular 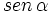 y
y 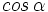 .
.
Hay que usar las relaciones fundamentales de la trigonometría para despejar la razón trigonométrica desconocida:
1. 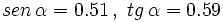
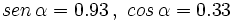
Razones trigonométricas de algunos ángulos importantes
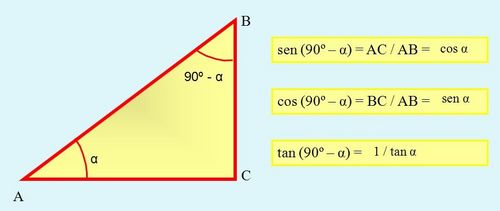
Razones trigonométricas de ángulos complementarios Sea Se cumple que: Relación entre el coseno, el seno y la tangente de ángulos complementarios. Relación entre el coseno y el seno de ángulos complementarios. Razones trigonométricas de ángulos complementarios:
Halla El rio Nilo se ha desbordado y ha inundado sus alrededores, a excepción de la punta de la pirámide de Guiza. Se ha enviado una expedición para averiguar la altura que alcanzó el agua. Los exploradores midieron el borde inclinado de la pirámide que quedó fuera del agua resultando ser de 72 m. Ellos saben además que la longitud total del borde es de 180 m y que la altura de la pirámide es de 139 m. ¿Cuál es la altura del agua sobre el nivel del suelo, redondeada a dos decimales? Razones trigonométricas de ángulos complementarios. |
Ejercicios propuestos
|
Ejercicios propuestos: Relaciones trigonométricas fundamentales |

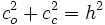
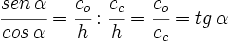
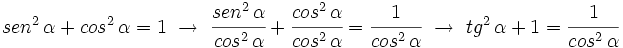
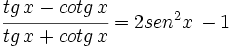
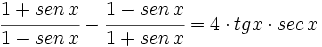
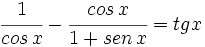
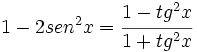
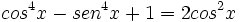
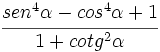
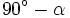 su complementario.
su complementario.
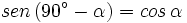
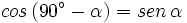
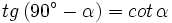
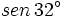 sabiendo que
sabiendo que 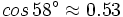 .
.