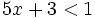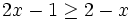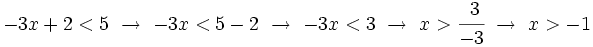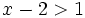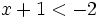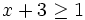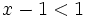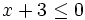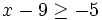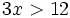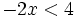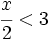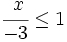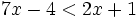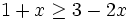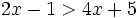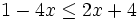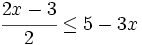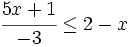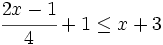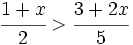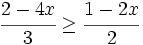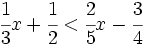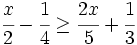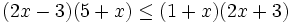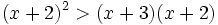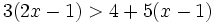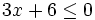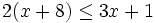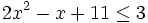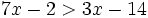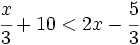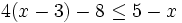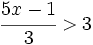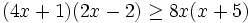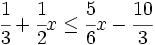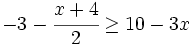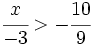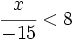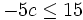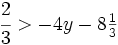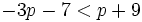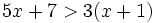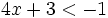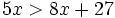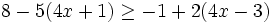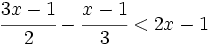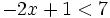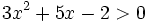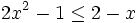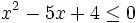Inecuaciones con una incógnita (1ºBach)
De Wikipedia
Revisión de 18:18 18 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Inecuación
- Una inecuación es una desigualdad entre expresiones algebraicas.
- Para las desigualdades utilizaremos los símbolos:
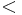 (menor que);
(menor que);  (mayor que);
(mayor que); 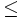 (menor o igual que) y
(menor o igual que) y 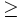 (mayor o igual que).
(mayor o igual que).
- Las inecuaciones que usan los dos primeros símbolos se llaman inecuaciones estrictas y las que utilizan los dos últimos, inecuaciones no estrictas.
- Si las expresiones algebraicas son polinomios de grado 1, las inecuaciones se llaman lineales y si son de grado 2, cuadráticas.
- Una solución de una inecuación es un conjunto de valores de las variables (uno de cada una) que hace que se cumpla la desigualdad.
- Resolver una inecuación consiste en hallar todas sus soluciones.
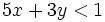 es una inecuación lineal estricta con dos incógnitas.
es una inecuación lineal estricta con dos incógnitas.
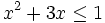 es una inecuación cuadrática no estricta con una incógnita.
es una inecuación cuadrática no estricta con una incógnita.
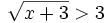 es una inecuación estricta con una incógnita.
es una inecuación estricta con una incógnita.
Qué son las inecuaciones.
Inecuaciones. Representación de sus soluciones en intervalos o gráficamente. Ejemplos.
Comprueba si los valores x=0, x=1, x=2 y x=5 son o no son soluciones de las inecuaciones siguientes:
- a)
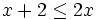
- b)
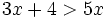
Verificar soluciones de inecuaciones.
Inecuaciones lineales con una incógnita
Una inecuación lineal con una incógnita es una inecuación, en la que las expresiones matemáticas que intervienen en la desigualdad, son polinomios de primer grado en una sola variable. En consecuencia, puede ponerse, mediante transformaciones, de alguna de estas formas:
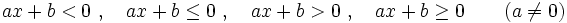
donde 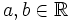 son los coeficientes y
son los coeficientes y  es la variable.
es la variable.
Resolución de una inecuación lineal con una incógnita
Método algebraico de resolución
El método algebraico aplica las anteriores transformaciones para conseguir dejar despejada la incógnita.
Ejemplo: Inecuaciones lineales con una incógnita (método algebraico)
Resuelve la siguiente inecuación:
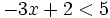
- Solución:
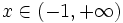
Inecuaciones de primer grado con una incógnita. Ejemplos.
Todo lo que necesitas saber para resolver inecuaciones de primer grado. Tutorial que explica de forma completa la resolución de inecuaciones de primer grado, empezando con algunos conceptos teóricos y resolviendo muchos ejericios desde muy sencillos, para entender mejor las propiedades de la regla de la suma y del producto.
- 00:00 a 09:00: Conceptos básicos. Definiciones. Desigualdades.
- 9:00 a 15:43: Reglas de la Suma y del Producto.
- 15:43 a 20:45: Ejemplos donde se aplica la regla del producto.
- 20:45 a 22:50: Algoritmo de resolución de inecuaciones de 1er grado.
- 22:50 a 32:41: Aplicación del algoritmo. Ejemplos resueltos.
Inecuaciones de primer grado con una incógnita. Ejemplos.
Inecuaciones de primer grado con una incógnita. Ejemplos.
Inecuaciones de primer grado con una incógnita. Ejemplos.
Inecuaciones de primer grado con una incógnita. Ejemplos.
Resuelve:
Resuelve:
Resuelve:
Resuelve:
Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: | Resuelve: Resuelve: Resuelve: a) b) c) Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve y representa gráficamente las soluciones:
Resuelve y representa gráficamente las soluciones: Resuelve y representa gráficamente las soluciones: Resuelve y representa gráficamente las soluciones: Resuelve y representa gráficamente las soluciones: Resuelve y representa gráficamente las soluciones:
Resuelve y representa gráficamente las soluciones: |
Un contratista está comprando baldosas de piedra para un patio. Cada baldosa cuesta $3, y quiere gastar menos de $1000. El tamaño de cada baldosa es de 1 pie cuadrado. Escribe una desigualdad que represente el número de baldosas que puede comprar y averigua cómo de grande puede ser el patio.
Una popular banda de blues regresó recientemente de una exitosa gira por tres ciudades donde tocaron para al menos 120 000 personas. Si tenían una audiencia de 45 000 en Ciudad de México y otras 33 000 en Guadalajara, ¿Qué puedes decir de las personas que asistieron en Acapulco?
En los últimos años, Granja Arce ha cosechado alrededor de 1000 manzanas más que su principal rival de la región, Huerto Rio Grande. Debido al clima frio de este año, la cosecha bajó en un tercio. Sin embargo, ambas granjas compensaron parte de ese déficit mediante la compra de cantidades iguales de manzanas de las granjas de estados vecinos.
- a) ¿Qué se puede decir del número de manzanas en cada granja?
- b) ¿Tiene una granja mayor cantidad de manzanas que la otra o tienen la misma cantidad? ¿Cómo lo sabes?
Autoevaluación sobre inecuaciones lineales de un paso.
Autoevaluación sobre inecuaciones lineales de dos pasos.
Autoevaluación sobre problemas de inecuaciones lineales de varios pasos.
Autoevaluación sobre problemas de inecuaciones lineales.
Autoevaluación sobre inecuaciones lineales.
Autoevaluación sobre inecuaciones lineales.
Autoevaluación sobre inecuaciones lineales sencillas.
Autoevaluación sobre inecuaciones lineales más complejas.
Método gráfico de resolución
Inecuaciones lineales con una incógnita (método gráfico)
Las soluciones de una inecuación lineal con una incógnita son los puntos de la semirrecta que se encuentra a uno de los dos lados del punto de corte de la recta 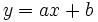 con el eje de abscisas, es decir del punto
con el eje de abscisas, es decir del punto 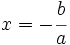 .
.
En una de las semirrectas con origen ese punto se cumple la condición 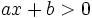 y en la otra, la condición
y en la otra, la condición 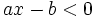 .
.
Así, para determinar la semirrecta solución, basta con fijarse en los valores de la variable x para los que la recta 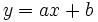 está por encima o por debajo del eje de abscisas.
está por encima o por debajo del eje de abscisas.
Si la inecuación no es estricta, el punto del extremo de la semirrecta, 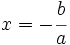 , es también solución, ya que para él se verifica la igualdad.
, es también solución, ya que para él se verifica la igualdad.
En la escena resolveremos la siguiente inecuación por el método gráfico:
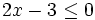
Para ello representamos la recta 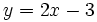 y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa) o vale cero.
y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa) o vale cero.
Inecuaciones cuadráticas con una incógnita
Una inecuación cuadrática con una incógnita es una inecuación en la que las expresiones matemáticas que intervienen en la desigualdad, son polinomios de segundo grado en una sola variable. En consecuencia, puede ponerse, mediante transformaciones, de alguna de estas formas:
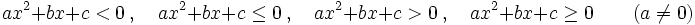
Resolución de inecuaciones cuadráticas con una incógnita
Para resolver estas inecuaciones usaremos el método gráfico. Este método requiere que el miembro de la derecha de la inecuación sea cero, lo cual siempre se puede conseguir mediante transformaciones.
Inecuaciones de segundo grado con una incógnita. Ejemplos.
Inecuaciones de segundo grado con una incógnita. Ejemplos.
Inecuaciones de segundo grado con una incógnita. Ejemplos.
Método: por intervalos (tabla de signos):
Resuelve:
- a)
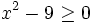
- b)
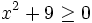
- c)
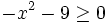
- d)
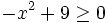
Resuelve: 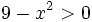
Resuelve: 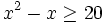
Resuelve: 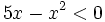
Resuelve: 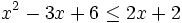
Resuelve: 
Resuelve: 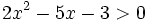
Resuelve: 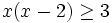
Resuelve: 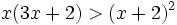
Resuelve: 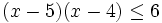
Resuelve: 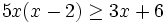
Método: analizando el signo de los factores / por intervalos:
Resuelve: 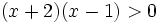 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 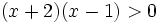 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 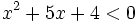 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 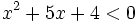 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 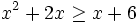 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 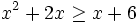 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 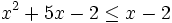 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 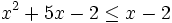 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 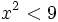 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 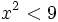 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 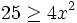 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 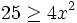 analizando el signo por intervalos.
analizando el signo por intervalos.
En la escena vamos a resolver la siguiente inecuación:
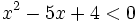
Representamos la parábola 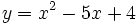 y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa).
y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa).
En realidad basta hallar los puntos de corte con el eje X y determinar la dirección de las ramas a partir del signo del coeficiente de 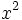 .
.
En este caso, los puntos de corte son 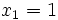 y
y 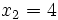 , soluciones de la ecuación de segundo grado
, soluciones de la ecuación de segundo grado
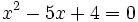
y las ramas va hacia arriba porque el coeficiente de 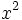 es positivo. Por tanto, las soluciones de la inecuación es:
es positivo. Por tanto, las soluciones de la inecuación es: 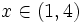 .
.
Puedes cambiar los valores A, B y C para resolver gráficamente otras inecuaciones de segundo grado.
Autoevaluación sobre inecuaciones cuadráticas.