Plantilla:Inecuaciones lineales con una incógnita
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:16 19 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:18 19 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| {{p}} | {{p}} | ||
| {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| - | Son inecuaciones linelaes con una incógnita: | + | Son inecuaciones lineales con una incógnita: |
| *<math>5x+3<1\;</math> | *<math>5x+3<1\;</math> | ||
Revisión de 19:18 19 ene 2009
- Una inecuación lineal con una incógnita es una inecuación que puede ponerse de alguna de estas formas:
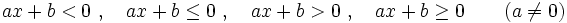 .
.
Ejemplos:
Son inecuaciones lineales con una incógnita:
Tabla de contenidos |
Resolución de inecuaciones lineales
Para resolverlas se procede de forma similar que con las ecuaciones de primer grado con una incógnita, aunque hay un pequeño matíz que las diferencia y que pasamos a explicar.
Transformaciones que mantienen la equivalencia de las inecuaciones
- Sumar o restar la misma expresión en los dos miembros de la desigualdad. (Así, lo que está sumando en un miembro, pasa restando al otro miembro. Y viceversa.)
- Multiplicar o dividir los dos miembros de la desigualdad por un mismo número mayor que cero. (Así, lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa.)
- Al multiplicar o dividir por un número negativo los dos miembros de la desigualdad, ésta cambia de sentido, es decir, pasa de ser (
 ó
ó 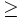 ) a (
) a (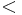 ó
ó 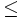 ), o viceversa.
), o viceversa.
Método algebraico de resolución
El método algebraico aplica las anteriores transformaciones para conseguir dejar despejada la incógnita.
Ejemplo: Inecuaciones lineales con una incógnita
Resuelve la siguiente inecuación:
<center>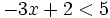
Solución:
- Solución:
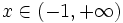
Método gráfico de resolución
El método gráfico requiere que el miembro de la derecha de la inecuación sea cero, lo cual puede conseguirse mediante las transformaciones antes mencionadas.
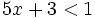
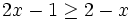
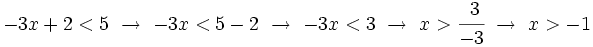
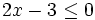
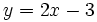 y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa) o vale cero.
y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa) o vale cero.
![x \in (- \infty, 1.5])](/wikipedia/images/math/6/c/9/6c98ec58684ed6f35d05405a20cba0d9.png)

