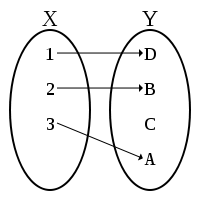
Función inyectiva
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:27 24 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:28 24 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | {{Desplegable|titulo=Ejemplo:{{b}}|contenido= |
| - | *La función <math>f:\mathbb{R}\to\mathbb{R}</math>, dada por <math>f(x)=x^2\,</math> no es inyectiva, puesto que <math>f(2)=f(-2)=4\;</math>. | + | La función <math>f:\mathbb{R}\to\mathbb{R}</math>, dada por <math>f(x)=x^2\,</math> no es inyectiva, puesto que <math>f(2)=f(-2)=4\;</math>. Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función <math>g:\mathbb{R}^+\to\mathbb{R}^+</math> entonces sí se obtiene una función inyectiva. |
| - | *Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función <math>g:\mathbb{R}^+\to\mathbb{R}^+</math> entonces sí se obtiene una función inyectiva. | + | |
| }} | }} | ||
| }} | }} | ||
Revisión de 17:28 24 ene 2009
Una función 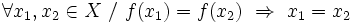 Ejemplo: La función 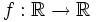 , dada por , dada por 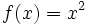 no es inyectiva, puesto que no es inyectiva, puesto que 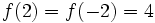 . Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función . Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función  entonces sí se obtiene una función inyectiva. entonces sí se obtiene una función inyectiva. |
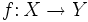 es inyectiva o uno a uno si cada valor en la imagen de
es inyectiva o uno a uno si cada valor en la imagen de  se corresponde con un único valor de su dominio. Simbólicamente:
se corresponde con un único valor de su dominio. Simbólicamente: