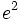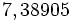Funciones exponenciales (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 14:34 25 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 14:48 25 ene 2009 Coordinador (Discusión | contribuciones) (→Función exponencial de base a) Ir a siguiente diferencia → |
||
| Línea 52: | Línea 52: | ||
| }} | }} | ||
| }} | }} | ||
| - | {{Tabla75 | + | {{p}} |
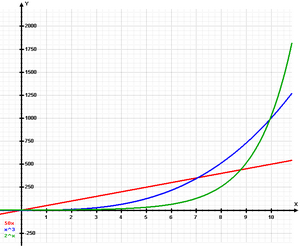
| - | |celda2=[[Image:Exponential.png|thumb|right|300px|Comparación entre el crecimiento lineal (rojo), crecimiento potencial (azul) y crecimiento exponencial (verde)]] | + | |
| - | |celda1={{p}} | + | |
| ===Propiedades=== | ===Propiedades=== | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| Línea 65: | Línea 63: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Tabla75 | ||
| + | |celda2=[[Image:Exponential.png|thumb|right|300px|Comparación entre el crecimiento lineal (rojo), crecimiento potencial (azul) y crecimiento exponencial (verde)]] | ||
| + | |celda1={{p}} | ||
| + | |||
| ===El crecimiento exponencial=== | ===El crecimiento exponencial=== | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| |texto=El término '''crecimiento exponencial''' se aplica generalmente a una magnitud <math>M\;</math> que crece con el tiempo <math>t\;</math> de acuerdo con la ecuación: | |texto=El término '''crecimiento exponencial''' se aplica generalmente a una magnitud <math>M\;</math> que crece con el tiempo <math>t\;</math> de acuerdo con la ecuación: | ||
| - | <center><math>M_t = M_0 \cdot a^{rt} \,</math></center> | + | <center><math>M_t = M_0 \cdot e^{rt} \,</math></center> |
| + | |||
| + | Donde: | ||
| + | *<math>M_t\;</math> es valor de la magnitud en el instante <math>t\;</math> > 0; | ||
| + | |||
| + | *<math>M_0\;</math> es el valor inicial de la variable, valor en <math>t = 0\;</math>, cuando empezamos a medirla; | ||
| + | |||
| + | *<math>r\;</math> es la llamada tasa de crecimiento instantánea, tasa media de crecimiento durante el lapso transcurrido entre <math>t = 0\;</math> y <math>t > 0\;</math>; | ||
| + | |||
| + | *<math>e = 2,718281828459...\;</math> | ||
| + | |||
| + | Esta expresión también podemos ponerla como una función exponencial de base <math>a\;</math> haciendo <math>r=ln(a)\;</math>. | ||
| + | |||
| + | <center><math>M_t=M_0 \cdot a^t\;</math></center> | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 81: | Línea 97: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Calculadora== | ==Calculadora== | ||
| {{Casio FX-100MS Exponencial}} | {{Casio FX-100MS Exponencial}} | ||
Revisión de 14:48 25 ene 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Función exponencial de base a
Sea 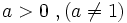 un número real. Se define la función exponencial de base
un número real. Se define la función exponencial de base  como:
como:
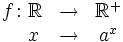
La función exponencial de base e (número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
|
Actividad Interactiva: Función exponencial
Actividad 1. Representación gráfica de distintas funciones exponenciales.
Actividad: En esta escena tienes las gráfica de las funciones: a)
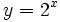 (en verde); b) (en verde); b) 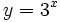 (en amarillo); c) (en amarillo); c) 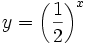 (en rojo); d) (en rojo); d) 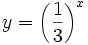 (en turquesa) (en turquesa)Comprueba en la escena anterior las siguientes propiedades:
|
Propiedades
Las funciones exponenciales de base  cumplen las siguientes propiedades:
cumplen las siguientes propiedades:
- Son continuas en
 .
.
- Pasan por
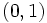 y
y 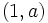 .
.
- Si
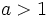 son crecientes y si
son crecientes y si 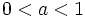 son decrecientes. Su crecicmiento supera al de cualquier función potencia.
son decrecientes. Su crecicmiento supera al de cualquier función potencia.
- Son positivas y nunca se anulan (su gráfica está por encima del eje X).
Calculadora
Exponencial de base 10
|
Calculadora: Exponencial de base 10 |
Exponencial de base e
|
Calculadora: Exponencial de base e |
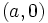 , donde
, donde 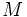 que crece con el tiempo
que crece con el tiempo 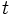 de acuerdo con la ecuación:
de acuerdo con la ecuación:
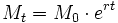
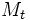 es valor de la magnitud en el instante
es valor de la magnitud en el instante 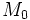 es el valor inicial de la variable, valor en
es el valor inicial de la variable, valor en 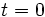 , cuando empezamos a medirla;
, cuando empezamos a medirla;
 es la llamada tasa de crecimiento instantánea, tasa media de crecimiento durante el lapso transcurrido entre
es la llamada tasa de crecimiento instantánea, tasa media de crecimiento durante el lapso transcurrido entre 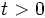 ;
;
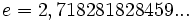
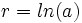 .
.
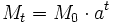
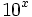 usaremos la tecla
usaremos la tecla 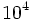
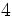
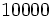
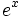 usaremos la tecla
usaremos la tecla