Semejanza de triángulos
De Wikipedia
| Revisión de 10:11 17 feb 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:13 17 feb 2009 Coordinador (Discusión | contribuciones) (→Teorema de Tales) Ir a siguiente diferencia → |
||
| Línea 62: | Línea 62: | ||
| </iframe></center> | </iframe></center> | ||
| <center>[http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411290954_PRE_0_-140273678&mode=1&rtc=1001&locale=es_ES&cache=false',600,400,'snrPop',0); '''Click''' aquí si no se ve bien la escena]</center> | <center>[http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411290954_PRE_0_-140273678&mode=1&rtc=1001&locale=es_ES&cache=false',600,400,'snrPop',0); '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 2:''' Enlaza la solución. | ||
| + | |actividad= | ||
| + | <center><iframe> | ||
| + | url=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411291000_AC_0_-750600157&mode=1&rtc=1001&locale=es_ES&cache=false',750,540,'snrPop',0); | ||
| + | width=790 | ||
| + | height=600 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411291000_AC_0_-750600157&mode=1&rtc=1001&locale=es_ES&cache=false',750,540,'snrPop',0); '''Click''' aquí si no se ve bien la escena]</center> | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 10:13 17 feb 2009
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Semejanza | WIRIS Geogebra Calculadora |
Tabla de contenidos |
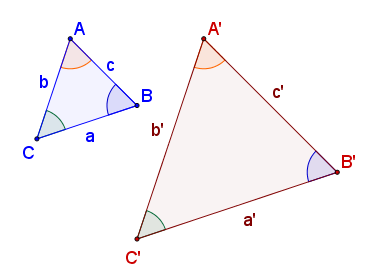
Triángulos semejantes
|
Actividad Interactiva: Triángulos semejantes
Actividad 1: Completa la tabla.
|
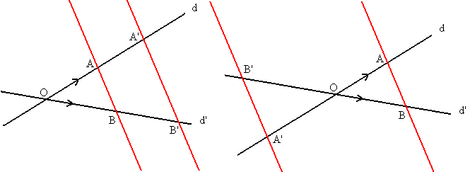
Teorema de Tales
Teorema de Tales
Dos rectas d y d', que se cortan en un punto O, cortadas por rectas paralelas AB y A'B', determinan segmentos proporcionales:
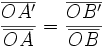 |
|
Actividad Interactiva: Teorema de Tales
Actividad 1: Los 100 metros lisos: Una aplicación del teorema de Tales.
Actividad 2: Enlaza la solución.
|
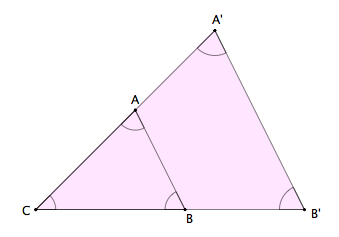
Triángulos en la posición de Tales
| Dos triángulos ABC y A'B'C', con sus lados paralelos y encajados con un vértice común, se dice que están en la posición de Tales |
Triángulos en la posición de Tales
Dos triángulos son semejantes si y sólo si están en la posición de Tales.
Observa la siguiente escena y mueve el punto verde para desplazar el triángulo amarillo. Podrás comprobar que los ángulos son iguales
Criterios de semejanza de triángulos
Criterios de semejanza de triángulos
- Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales:
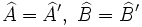
- Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido:
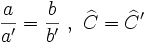
- Dos triángulos son semejantes si tienen los lados proporcionales:
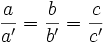
- En efecto, si tienen dos ángulos respectivamente iguales, el tercero también lo tienen igual. Entonces, esos dos triángulos se pueden poner en la posición de Tales y, en consecuencia, son semejantes.
Aplicaciones de los criterios de semejanza
|
Actividad Interactiva: Aplicaciones de los criterios de semejanza
Actividad 1: Cálculo de la altura conocida la sombra.
Actividad: La distancia del Sol a la Tierra es muy grande comparada con la tierra y con los objetos que hay sobre ella, de forma que podemos considerar que los rayos del Sol sobre objetos próximos son paralelos. En consecuencia, los triángulos que forma tienen sus ángulos iguales y, por tanto, son semejantes. Entonces, al ser los lados de los triángulos proporcionales, tenemos: 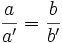 expresión de la cual, conocidos 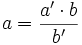
Actividad 2: Halla la altura de un árbol con la ayuda de un espejo y una cinta métrica.
Actividad: Los triángulos ABC y A'BC' son semejantes. ¿Por qué? En el punto B se coloca un espejo de forma que desde A se vea el extremo del árbol a través de él. Calcula la altura del árbol. Pon como distancia AC tu estatura y sitúa el punto C donde te parezca más conveniente. La altura calculada ¿depende de la altura del observador y de donde se sitúe?
Actividad 3: Semejanza en triángulos rectángulos.
Actividad: El triángulo ABC es rectángulo, y también lo son los triángulos ACM y BCM. Toma las medidas que necesites para comprobar que los dos triángulos coloreados son semejantes. También se puede comprobar que son semejantes si nos fijamos en sus ángulos. ¿Por qué? Además, cada uno de ellos de los dos triángulos es también semejante al triángulo ABC. ¿Por qué? |
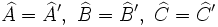
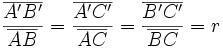
 , se la razón de semejanza.
, se la razón de semejanza.
 ,
,  y
y  , podemos despejar
, podemos despejar 
