Paralelismo y perpendicularidad en el plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:51 19 mar 2009 Coordinador (Discusión | contribuciones) (→Perpendicularidad) ← Ir a diferencia anterior |
Revisión de 11:57 19 mar 2009 Coordinador (Discusión | contribuciones) (→Perpendicularidad) Ir a siguiente diferencia → |
||
| Línea 27: | Línea 27: | ||
| {{p}} | {{p}} | ||
| |actividad=Las ecuaciones de las rectas que aparecen en la siguiente escena son: | |actividad=Las ecuaciones de las rectas que aparecen en la siguiente escena son: | ||
| - | + | {{Tabla3 | |
| - | *En azul: <math> | + | |celda1=En azul: <math> |
| \begin{cases} | \begin{cases} | ||
| x=3+ 5t | x=3+ 5t | ||
| Línea 34: | Línea 34: | ||
| y=7-2t | y=7-2t | ||
| \end{cases} | \end{cases} | ||
| - | \quad \rightarrow \quad \overrightarrow{d}=(5,-2) | ||
| </math> | </math> | ||
| - | *En rojo: <math> | + | {{p}} |
| + | <math> | ||
| + | \overrightarrow{d}=(5,-2) | ||
| + | </math> | ||
| + | |celda2=En rojo: <math> | ||
| \begin{cases} | \begin{cases} | ||
| x=6+ 5t | x=6+ 5t | ||
| Línea 42: | Línea 45: | ||
| y=4-2t | y=4-2t | ||
| \end{cases} | \end{cases} | ||
| - | \quad \rightarrow \quad \overrightarrow{d}=(5,-2) | ||
| </math> | </math> | ||
| - | *En verde: <math> | + | {{p}} |
| + | <math> | ||
| + | \overrightarrow{d}=(5,-2) | ||
| + | </math> | ||
| + | |celda3=En verde: <math> | ||
| \begin{cases} | \begin{cases} | ||
| x=6-2t | x=6-2t | ||
| Línea 50: | Línea 56: | ||
| y=4-5t | y=4-5t | ||
| \end{cases} | \end{cases} | ||
| - | \quad \rightarrow \quad \overrightarrow{d}=(-2,-5) | + | </math> |
| - | </math> | + | {{p}} |
| + | <math> | ||
| + | \overrightarrow{d}=(-2,-5) | ||
| + | </math> | ||
| + | }} | ||
| + | |||
| + | Observa cómo son los vectores de dirección: | ||
| + | |||
| + | *Los dos primeros iguales a (5,-2)(rectas paralelas). | ||
| + | *El tercero ortogonal con los dos primeros: <math>(5,-2) \cdot (-2,-5)=0</math> (rectas perpendiculares) | ||
| - | Observa cómo son los vectores de dirección: Los dos primeros iguales (rectas paralelas) | ||
| - | Y el último ortogonal con los dos primeros: <math>(5,-2) \cdot (-2,-5)=0</math> | ||
| <center><iframe> | <center><iframe> | ||
| url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_5_2.html | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_5_2.html | ||
Revisión de 11:57 19 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Paralelismo
He aquí dos criterios para determinar si dos rectas son paralelas:
- Dos rectas son paralelas si tienen la misma dirección y ésto ocurre cuando sus vectores de dirección son iguales o proporcionales.
- Dos rectas son paralelas si sus pendientes coinciden:
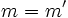 .
.
Perpendicularidad
He aquí dos criterios para determinar si dos rectas son perpendiculares:
- Dos rectas son perpendiculares si sus vectores de dirección son ortogonales, o lo que es lo mismo, si el producto escalar de sus vectores de dirección es cero. Traduciendo ésto a coordenadas: Dos rectas con vectores de dirección
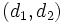 y
y 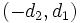 son perpendiculares.
son perpendiculares.
- Dos rectas son perpendiculares si sus pendientes
 y
y 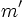 cumplen que:
cumplen que: 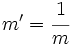 .
.
|
Actividad interactiva: Paralelismo y perpendicularidad Actividad 1: En la siguiente escena nos dan las ecuaciés paramétricas de tres rectas que son paralelas o perpendiculares entre sí. Actividad: Las ecuaciones de las rectas que aparecen en la siguiente escena son:
Observa cómo son los vectores de dirección:
|
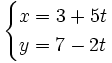
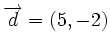
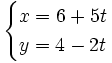
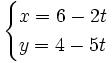
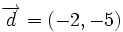
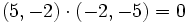 (rectas perpendiculares)
(rectas perpendiculares)

