Las cónicas (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 14:23 27 mar 2009 Coordinador (Discusión | contribuciones) (→Secciones cónicas) ← Ir a diferencia anterior |
Revisión de 16:24 27 mar 2009 Coordinador (Discusión | contribuciones) (→Secciones cónicas) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| {{Tabla75|celda2=[[Imagen:Cono y secciones.jpg|220px|center]] | {{Tabla75|celda2=[[Imagen:Cono y secciones.jpg|220px|center]] | ||
| |celda1= | |celda1= | ||
| - | {{Caja_Amarilla|texto=Se denomina '''sección cónica''' a la curva intersección de un cono con un plano que no pasa por su vértice. Según como corte el plano al cono tendremos (ver figura): | + | {{Caja_Amarilla|texto=Se denomina '''sección cónica''' a la curva intersección de un cono con un plano que no pasa por su vértice. |
| + | |||
| + | Según como corte el plano al cono tendremos (ver figura): | ||
| + | |||
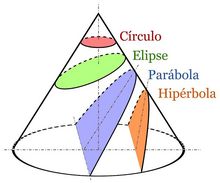
| *'''Hipérbola:''' el plano forma con la base un ángulo mayor que el que forma la generatriz. | *'''Hipérbola:''' el plano forma con la base un ángulo mayor que el que forma la generatriz. | ||
| - | *'''Parábola:''' el plano es paralelo a la generatriz | + | *'''Parábola:''' el plano es paralelo a la generatriz. |
| *'''Elipse:''' el plano forma con la base un ángulo menor que el que forma la generatriz. | *'''Elipse:''' el plano forma con la base un ángulo menor que el que forma la generatriz. | ||
| - | *'''Circunferencia:''' el plano es paralelo a la base | + | *'''Circunferencia:''' el plano es paralelo a la base. |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 16:24 27 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Secciones cónicas
Se denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. Según como corte el plano al cono tendremos (ver figura):
La primera definición de sección cónica aparece en Grecia, cerca del año 350, donde las definieron como secciones de un cono circular recto. Los nombres de hipérbola, parábola y elipse se deben a Apolonio. |