Números enteros
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:44 12 abr 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:55 12 abr 2007 Coordinador (Discusión | contribuciones) (→Problemas) Ir a siguiente diferencia → |
||
| Línea 123: | Línea 123: | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | '''1. '''Calcula: | + | '''1. '''Un caracol está en el fondo de un pozo de 10m de profundidad. Para salir del pozo, asciende 3 m cada día, pero por la noche descende 2 m. ¿Cuántos días tardará en llegar al borde del pozo? |
| - | + | ||
| - | :a) <math>9+4\cdot7-2=</math> | + | |
| - | + | ||
| - | :b) <math>(9+4)\cdot7-2=</math> | + | |
| - | + | ||
| - | :c) <math>9+4\cdot(7-2)=</math> | + | |
| - | + | ||
| - | :d) <math>(9+4)\cdot(7-2)=</math> | + | |
| - | <p></p> | + | |
| |sol= | |sol= | ||
| - | a) 35{{b}}b) 89{{b}}c) 29{{b}}d) 65 | + | 8 días. |
| }} | }} | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | '''2. '''En una división, el dividendo es 969, el cociente 74, y el resto 7. ¿Cúal es el divisor? | + | '''2.''' Calcula la diferencia de altura entre el Everest, que mide 8.848 m, y la fosa de las Marianas, que llega a -11022 m. |
| |sol= | |sol= | ||
| - | El divisor es 13 | + | 19.870 m. |
| }} | }} | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | '''3. '''Un ganadero compra una vaca por 1400 €. Cada día, por término medio, obtiene 21 litros de leche, que vende a 47 céntimos el litro. La vaca consume cada día unos 8 kg de pienso, que sale a 76 céntimos el kg. Al cabo de 180 días la vende por 1200 €. ¿Qué beneficio ha obtenido? | + | '''3. '''La temperatura de un congelador desciende 2 grados cada 5 minutos hasta llegar a -20ºC. ¿Cuánto tardará en llegar a -12ºC si, cuando lo enchufamos, la temperatura es de 18ºC? |
| |sol= | |sol= | ||
| - | }} | ||
| - | {{ejercicio_cuerpo | ||
| - | |enunciado= | ||
| - | |||
| - | '''4. '''Simplifica: | ||
| - | |||
| - | :a) <math>(x^3)^4\,\!</math>{{b}}b) <math>x^2 \cdot x^2 \cdot x^2</math>{{b}}c) <math>(a^3)^2 \cdot (a^2)^5 \cdot a</math> | ||
| - | <p></p> | ||
| - | |sol= | ||
| - | a) <math>x^{12}\,\!</math>{{b}}b) <math>x^6\,\!</math>{{b}}c) <math>a^{17}\,\!</math> | ||
| - | |||
| - | }} | ||
| - | {{ejercicio_cuerpo | ||
| - | |enunciado= | ||
| - | |||
| - | '''5. '''Simplifica: | ||
| - | |||
| - | :a) <math>\cfrac{2^5}{2^3}</math>{{b}}b) <math>\cfrac{3^4}{3^2}</math>{{b}}c) <math>\cfrac{2^3 \cdot 3^4}{2 \cdot 3}</math> | ||
| - | <p></p> | ||
| - | |sol= | ||
| - | a) <math>2^2\,\!</math>{{b}}b) <math>3^2\,\!</math>{{b}}c) <math>2^2 \cdot 3^3</math> | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 19:55 12 abr 2007
Menú:
| Ir a | Para repasar | Para ampliar | Herramientas |
| Indice | Números enteros I | Números enteros | WIRIS Calculadora |
Tabla de contenidos |
Definición
El conjunto de los números enteros es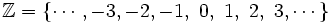 
. Son infinitos y, al igual que los números naturales sirven para contar. Sin emabrgo, los números enteros permiten expresar cantidades negativas como un saldo deudor en una cuenta bancaria, un año de la era antes de Cristo, el número de una planta del sótano de un edificio, etc.
Podemos representarlos en una recta:
Orden
En el gráfico anterior se observa el orden que existe en el conjunto de los números enteros, siendo los números negativos menores que los positivos y que el cero. Se cumple que:
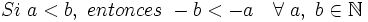
Operaciones
Valor absoluto
Opuesto
Suma
Uso del paréntesis
Actividad Interactiva: Uso del paréntesis
