Factoriales y números combinatorios (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:49 4 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:55 4 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Factoriales== | ==Factoriales== | ||
| - | {{Caja Amarilla|texto=El '''factorial''' de un número entero positivo "n" es el número | + | {{Caja Amarilla|texto=*El '''factorial''' de un número entero positivo "n" es el número |
| {{p}} | {{p}} | ||
| <center><math>n! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot ... \cdot n = \prod_{k=1}^n k | <center><math>n! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot ... \cdot n = \prod_{k=1}^n k | ||
| </math></center> | </math></center> | ||
| + | |||
| + | *Se define, por convenio, <math>0! = 1 \;</math>. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 17: | Línea 19: | ||
| :<math>5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 = 120</math> | :<math>5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 = 120</math> | ||
| }} | }} | ||
| + | La operación de factorial aparece en muchas áreas de las matemáticas, particularmente en [[combinatoria]] y [[análisis matemático]]. | ||
| + | De manera fundamental el factorial de ''n'' representa el número de formas distintas de ordenar ''n'' objetos distintos (elementos sin repetición). Este hecho ha sido conocido desde hace varios siglos, en el siglo XII por los estudiosos [[India|hindúes]]. | ||
| + | |||
| + | La notación matemática actual ''n''! fue usada por primera vez en 1808 por [[Christian Kramp]] (1760–1826), un matemático francés que trabajó, en especial, sobre los factoriales durante toda su vida. | ||
| + | |||
| ==Números combinatorios== | ==Números combinatorios== | ||
Revisión de 10:55 4 sep 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Factoriales
- El factorial de un número entero positivo "n" es el número
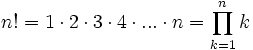
- Se define, por convenio,
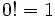 .
.
La operación de factorial aparece en muchas áreas de las matemáticas, particularmente en combinatoria y análisis matemático. De manera fundamental el factorial de n representa el número de formas distintas de ordenar n objetos distintos (elementos sin repetición). Este hecho ha sido conocido desde hace varios siglos, en el siglo XII por los estudiosos hindúes.
La notación matemática actual n! fue usada por primera vez en 1808 por Christian Kramp (1760–1826), un matemático francés que trabajó, en especial, sobre los factoriales durante toda su vida.