Plantilla:Raiz de 2 no es racional
De Wikipedia
| Revisión de 13:04 7 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 13:04 7 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| Multiplicamos por {{sube|porcentaje=+20%|contenido=<math>b^2\;\!</math>}} los dos miembros de la igualdad: | Multiplicamos por {{sube|porcentaje=+20%|contenido=<math>b^2\;\!</math>}} los dos miembros de la igualdad: | ||
| - | <center><math>a^2=2 \cdot b^2</math></center> [1] | + | <center><math>a^2=2 \cdot b^2</math> [1]</center> |
| Sabemos que en la descomposición factorial de un cuadrado perfecto, distinto de 1, todos los factores que aparecen lo hacen un número par de veces. | Sabemos que en la descomposición factorial de un cuadrado perfecto, distinto de 1, todos los factores que aparecen lo hacen un número par de veces. | ||
Revisión de 13:04 7 sep 2016
Proposición
- No existe ningún número racional que elevado al cuadrado dé como resultado 2. Es decir, el número
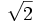no es racional.
Vamos ha utilizar un tipo de demostración denominado "por reducción al absurdo". Supondremos que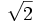 es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
Por tanto, supongamos que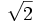 es racional, o sea, que existe una fracción de números enteros 
que es igual a.
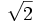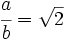
Elevamos al cuadrado los dos miembros de la igualdad:
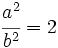
Multiplicamos por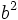 
los dos miembros de la igualdad:
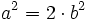[1]Sabemos que en la descomposición factorial de un cuadrado perfecto, distinto de 1, todos los factores que aparecen lo hacen un número par de veces.
Como 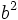es un cuadrado perfecto, el factor 2 o no aparece o lo hace un número par de veces. Pero entonces, el factor 2 aparecería un número impar de veces en la descomposición del cuadrado perfecto 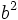por [1].
