Número áureo
De Wikipedia
| Revisión de 07:25 8 sep 2016 Coordinador (Discusión | contribuciones) (→Rectángulo áureo) ← Ir a diferencia anterior |
Revisión de 12:11 8 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| ==El número áureo== | ==El número áureo== | ||
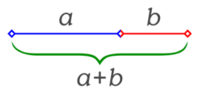
| - | {{Tabla75|celda2=[[Imagen:Image-Golden ratio line.png|200px|thumb|El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total <font color="green">'''''a+b'''''</font> es al segmento más largo <font color="blue">'''''a'''''</font>, como <font color="blue">'''''a'''''</font> es al segmento más corto <font color="red">'''''b'''''</font>.]] | + | {{Tabla75|celda2=[[Imagen:Image-Golden ratio line.png|200px|thumb|''Fig.1'' El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total <font color="green">'''''a+b'''''</font> es al segmento más largo <font color="blue">'''''a'''''</font>, como <font color="blue">'''''a'''''</font> es al segmento más corto <font color="red">'''''b'''''</font>.]] |
| |celda1={{Caja_Amarilla|texto= | |celda1={{Caja_Amarilla|texto= | ||
| El '''número áureo''', es el primer [[Números irracionales|número irracional]] del que se tuvo conciencia de que lo era. Su valor es: | El '''número áureo''', es el primer [[Números irracionales|número irracional]] del que se tuvo conciencia de que lo era. Su valor es: | ||
| Línea 39: | Línea 39: | ||
| ==Rectángulo áureo== | ==Rectángulo áureo== | ||
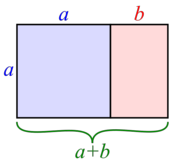
| - | {{Tabla75|celda2=[[Imagen:rectangulos_aureos.png|thumb|Fig. 2 Si en un rectángulo áureo substraemos la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es también un rectángulo áureo.]] | + | {{Tabla75|celda2=[[Imagen:rectangulos_aureos.png|thumb|''Fig.2'' Si en un rectángulo áureo substraemos la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es también un rectángulo áureo.]] |
| |celda1= | |celda1= | ||
| {{Caja_Amarilla|texto=El '''rectángulo áureo''' (o rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual al '''número áureo'''.}} | {{Caja_Amarilla|texto=El '''rectángulo áureo''' (o rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual al '''número áureo'''.}} | ||
| Línea 64: | Línea 64: | ||
| }} | }} | ||
| ===Construcción del rectángulo áureo=== | ===Construcción del rectángulo áureo=== | ||
| - | {{Tabla75|celda2=[[Imagen:Golden Rectangle Construction.png|thumb|Construcción del rectángulo áureo con regla y compás .]] | + | {{Tabla75|celda2=[[Imagen:Golden Rectangle Construction.png|thumb|''Fig.3'' Construcción del rectángulo áureo con regla y compás .]] |
| |celda1= | |celda1= | ||
| {{Teorema|titulo=Construcción del rectángulo áureo con regla y compás|enunciado= | {{Teorema|titulo=Construcción del rectángulo áureo con regla y compás|enunciado= | ||
| Línea 74: | Línea 74: | ||
| # Ese punto obtenido determina la base del rectángulo áureo con altura igual al lado del cuadrado. | # Ese punto obtenido determina la base del rectángulo áureo con altura igual al lado del cuadrado. | ||
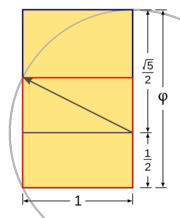
| |demo= Si te fijas en la Fig. 3, basta con demostrar que el segmento que se obtiene en el paso 2 mide <math>\cfrac{\sqrt{5}}{2}</math>, para lo cual basta con usar el teorema de Pitágoras. | |demo= Si te fijas en la Fig. 3, basta con demostrar que el segmento que se obtiene en el paso 2 mide <math>\cfrac{\sqrt{5}}{2}</math>, para lo cual basta con usar el teorema de Pitágoras. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Construccion numero aureo}} | ||
| + | }} | ||
| + | {{p}} | ||
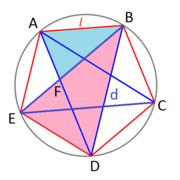
| + | ==El número áureo en el péntágono estrellado== | ||
| + | {{Tabla75|celda2=[[Imagen:Pentagono_estrellado.png|thumb|''Fig.4'' Petágono estrellado.]] | ||
| + | |celda1= | ||
| + | {{Teorema|titulo=El número áureo en el péntágono estrellado|enunciado=:La razón entre la diagonal del del péntagono regular y su lado es igual al número áureo. (Ver Fig.4 ) | ||
| + | <br> | ||
| + | <center><math>\cfrac{d}{l}= \phi</math></center> | ||
| + | |demo= | ||
| + | *Los triángulos ABF y EBD son semejantes ya que tienen sus ángulos iguales. Para comprobarlo basta aplicar la propiedad que dice que los ángulos inscritos en una circunferencia que abarcan el mismo arco son iguales. | ||
| + | *Por ser semejantes los triángulos ABF y EBD, sus lados son proporcionales: | ||
| + | {{p}} | ||
| + | <center><math>\cfrac{l}{d}=\cfrac{d-l}{l} \ \rightarrow \ \cfrac{l}{d}=\cfrac{d}{l}-1 \ \rightarrow \ \cfrac{1}{{d \over l}}=\cfrac{d}{l}-1</math></center> | ||
| + | {{p}} | ||
| + | Haciendo el cambio de variable <math>x= \cfrac{d}{l}</math>: | ||
| + | |||
| + | <center><math>\cfrac{1}{x}=x+1 \ \rightarrow \ x^2-x-1=0 \ \rightarrow \ x=\frac{1 + \sqrt{5}}{2} = \phi</math></center> | ||
| + | {{p}} | ||
| + | c.q.d. | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 12:11 8 sep 2016
Tabla de contenidos |
El número áureo
El número áureo, es el primer número irracional del que se tuvo conciencia de que lo era. Su valor es: 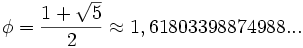 Es representado por la letra griega phi φ (en minúscula) o Φ (en mayúscula) en honor al escultor griego Fidias. También se le conoce como número de oro, razón áurea o divina proporción (por la obra de Luca Pacioli, De Divina Proportione, escrito entre 1496 y 1498). Proposición 1
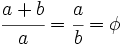 Demostración: Partimos de la proporción dada: 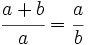 Separamos en dos sumandos el término de la izquierda: 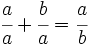 Llamando 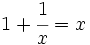 Quitando denominadores y trasponiendo términos: 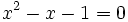 ecuación de segundo grado cuya única raíz válida es: 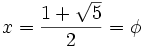 |
Rectángulo áureo
El rectángulo áureo (o rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual al número áureo. Los griegos consideraban que un rectángulo de tales características era especialmente armonioso. Esta proporción de medidas se ha utilizado con mucha frecuencia en el arte. Proposición 2
Demostración: Partimos de un rectángulo áureo. Lo dividimos en un cuadrado de lado su lado menor y otro rectángulo pequeño, como se observa en la Fig. 2. Veamos que el rectángulo pequeño también es un rectángulo áureo. Para ello tendremos que comprobar que Por ser el rectángulo de partida un rectángulo áureo, se cumple que la proporción entre sus lados es el número áureo: 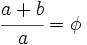 Operando:
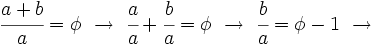 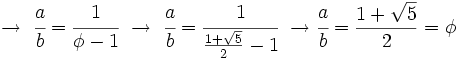 |
Construcción del rectángulo áureo
Construcción del rectángulo áureo con regla y compás
Demostración: Si te fijas en la Fig. 3, basta con demostrar que el segmento que se obtiene en el paso 2 mide 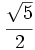 , para lo cual basta con usar el teorema de Pitágoras. , para lo cual basta con usar el teorema de Pitágoras.En la escena puedes ver la construcción del número de oro basada en una construcción gráfica que se encuentra en un libro de Euclides (siglo III a.C.).
Construcción con regla y compás de la sección áurea de un segmento y del rectángulo áureo. |
El número áureo en el péntágono estrellado
El número áureo en el péntágono estrellado
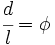 Demostración:
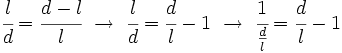 Haciendo el cambio de variable 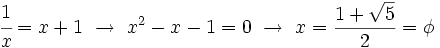 En la escena puedes ver la construcción del número de oro basada en una construcción gráfica que se encuentra en un libro de Euclides (siglo III a.C.).
Construcción con regla y compás de la sección áurea de un segmento y del rectángulo áureo. |
Videos y páginas web
Documental sobre el número aureo.
El programa presenta a este exótico número ya conocido por los griegos. Veremos cómo se obtiene, qué son los rectángulos áureos y su presencia en infinidad de manifestaciones artísticas, en Pintura, Arquitectura, Escultura... a lo largo de la historia. Pero el número de oro no es un mero invento del hombre, la naturaleza nos sorprende de una forma que no puede ser casual, tanto en el mundo vegetal como en el animal, como en multitud de fenómenos físicos, con acontecimientos en los que este famosos número hace acto de presencia.
A lo largo de la historia, Phi, el número de oro o número áureo, ha representado, para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino. ¿Por qué?. Página elaborada por D. Luis Nicolás Ortiz.
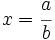 , tenemos que
, tenemos que 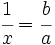 , de manera que:
, de manera que:
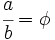
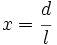 :
: