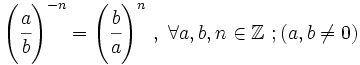Plantilla:Potencias de números fraccionarios
De Wikipedia
| Revisión de 07:26 13 sep 2016 Coordinador (Discusión | contribuciones) (→Potencias de exponente negativo) ← Ir a diferencia anterior |
Revisión de 07:27 13 sep 2016 Coordinador (Discusión | contribuciones) (→Potencias de exponente negativo) Ir a siguiente diferencia → |
||
| Línea 23: | Línea 23: | ||
| {{Def potencia exponente entero}} | {{Def potencia exponente entero}} | ||
| {{p}} | {{p}} | ||
| - | {{AI potencias expnente entero}} | + | {{AI potencias exponente entero}} |
Revisión de 07:27 13 sep 2016
Potencias de números fraccionarios
Las potencias con números racionales cumplen las mismas propiedades que con números naturales y enteros.Pulsa los botones para obtener ejemplos de cada tipo:
Tan sólo queda añadir el siguiente caso:
Potencias de exponente negativo
Se define la potencia de exponente negativo como:

Como consecuencia:
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos.
 . Ejemplos.
. Ejemplos.
Exponentes negativos. Ejemplos.
Razonando sobre el por qué de la definición de los exponentes negativos.
Simplifica:
- a)
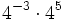
- b)
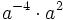
- c)
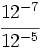
- d)
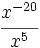
Simplifica:
- a)
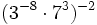
- b)
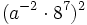
- c)
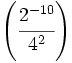
Halla el valor de:
11) 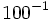 ; 12)
; 12) 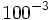 ; 13)
; 13) 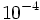 ; 14)
; 14) 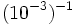
15) 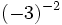 ; 16)
; 16) 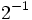 ; 17)
; 17) 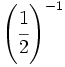 ; 18)
; 18) 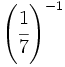 ; 19)
; 19) 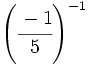
Potencias de exponente negativo.
Actividades sobre potencias de exponente negativo.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) 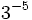 b)
b) 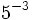 c)
c) 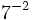 d)
d) 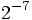
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba.
Potencias de exponente negativo.
Multiplica y divide potencias (exponentes enteros).
Potencias de productos y cocientes (exponentes enteros)
Potencias de exponentes enteros.
Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien.
Ejercicios de autoevaluación sobre potencias de exponente negativo.