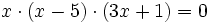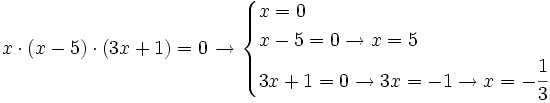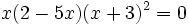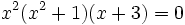Plantilla:Ecuaciones factorizadas
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:36 9 sep 2016 Coordinador (Discusión | contribuciones) (→Resolución de las ecuaciones factorizadas) ← Ir a diferencia anterior |
Revisión de 12:19 18 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| |titulo=Resolución de las ecuaciones factorizadas | |titulo=Resolución de las ecuaciones factorizadas | ||
| |enunciado= | |enunciado= | ||
| - | :Como para que un producto de números reales sea cero basta con que uno de ellos sea cero, las soluciones se obtendrán igualando a cero cada uno de los factores y resolviendo la ecuación resultante. Dependiendo de como sea cada factor tendremos que aplicar alguna de las distintas técnicas estudiadas anteriormente. | + | Como para que un producto de números reales sea cero basta con que uno de ellos sea cero, las soluciones se obtendrán igualando a cero cada uno de los factores y resolviendo la ecuación resultante. Dependiendo de como sea cada factor tendremos que aplicar alguna de las distintas técnicas estudiadas anteriormente. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | |||
| {{Ejemplo|titulo=Ejemplo: ''Ecuación factorizada'' | {{Ejemplo|titulo=Ejemplo: ''Ecuación factorizada'' | ||
| - | |enunciado=:Resuelve la ecuación <math> x \cdot (x-5)\cdot (3x+1)=0\;\!</math> | + | |enunciado=Resuelve la ecuación <math> x \cdot (x-5)\cdot (3x+1)=0\;\!</math> |
| |sol= | |sol= | ||
| Línea 31: | Línea 30: | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| + | Resuelve las siguientes ecuaciones: | ||
| - | :Resuelve las siguientes ecuaciones: | + | :a) <math>x(2-5x)(x+3)^2=0 \;</math> |
| - | + | ||
| - | ::a) <math>x(2-5x)(x+3)^2=0 \;</math> | + | |
| - | ::b) <math>x^2(x^2+1)(x+3)=0 \;</math> | + | :b) <math>x^2(x^2+1)(x+3)=0 \;</math> |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
Revisión de 12:19 18 sep 2016
Resolución de las ecuaciones factorizadas
Resolución de las ecuaciones factorizadas
Como para que un producto de números reales sea cero basta con que uno de ellos sea cero, las soluciones se obtendrán igualando a cero cada uno de los factores y resolviendo la ecuación resultante. Dependiendo de como sea cada factor tendremos que aplicar alguna de las distintas técnicas estudiadas anteriormente.
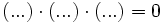
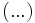 es una
es una