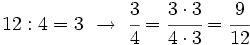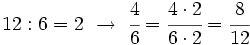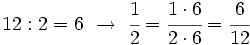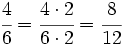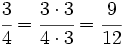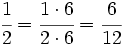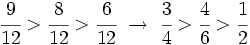Fracciones: Reducción a común denominador (1º ESO)
De Wikipedia
| Revisión de 16:07 25 sep 2016 Coordinador (Discusión | contribuciones) (→Reducción de fracciones a común denominador) ← Ir a diferencia anterior |
Revisión de 16:22 25 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 46: | Línea 46: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==Comparación de fracciones== | ||
| + | Vimos que una fdrma de comparar fracciones consistía en calcular su valor numérico, efectuando la división. Vamos a ver otro procedimiento: | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado=Para comparar fracciones, primero las reduciremos a común denominador y luego las ordenaremos comparando los numeradores.}} | ||
| + | {{p}} | ||
| + | {{Ejemplo|titulo=Ejemplo: ''Comparación de fracciones'' | ||
| + | |enunciado= | ||
| + | Ordena las siguientes fracciones: <math>\cfrac{4}{6} \, , \ \cfrac{3}{4} \, \ y \ \cfrac{1}{2}</math> | ||
| + | |sol= | ||
| + | Calculamos el m.c.m. de los denominadores: | ||
| + | {{p}} | ||
| + | :<math>m.c.m.(4, 6, 2)=12\;\!</math>. | ||
| + | {{p}} | ||
| + | A continuación, las reducimos a común denominador: | ||
| + | {{p}} | ||
| + | :<math>\cfrac{4}{6} = \cfrac{4 \cdot 2}{6 \cdot 2} =\cfrac{8}{12}</math> | ||
| + | {{p}} | ||
| + | :<math>\cfrac{3}{4} = \cfrac{3 \cdot 3}{4 \cdot 3} =\cfrac{9}{12}</math> | ||
| + | {{p}} | ||
| + | :<math>\cfrac{1}{2} = \cfrac{1 \cdot 6}{2 \cdot 6} =\cfrac{6}{12}</math> | ||
| + | Ordenamos las fracciones obtenidas, y a partir de ellas las fracciones de partida: | ||
| + | |||
| + | :<math>\cfrac{9}{12} > \cfrac{8}{12} > \cfrac{6}{12} \ \rightarrow \ \cfrac{3}{4} > \cfrac{4}{6} > \cfrac{1}{2}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
| {{ejercicio | {{ejercicio | ||
Revisión de 16:22 25 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 136)
Reducción de fracciones a común denominador
Comparar o sumar fracciones resulta mucho más fácil si éstas vienen dadas con el mismo denominador. Esto lo podemos conseguir gracias a la equivalencia de fracciones, como vamos a ver a continuación:
Reducir fracciones a común denominador consiste en sustituirlas por otras equivalentes con el mismo denominador.
Procedimiento
Para reducir fracciones a común denominador, eligiremos como denominador a un múltiplo común de todos los denominadores. Normalmente se elige el m.c.m. de ellos.
Ejemplo: Reducción de fracciones a común denominador
Reduce a común denominador las fracciones: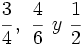 
Calculamos el m.c.m. de los denominadores:
.
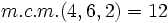A continuación, multiplicaremos el numerador y denominador de cada fracción por el resultado de dividir ese m.c.m. por el denominador de cada fracción:
Actividades: Reducción a común denominador Descripción: Comparación de fracciones
Vimos que una fdrma de comparar fracciones consistía en calcular su valor numérico, efectuando la división. Vamos a ver otro procedimiento:
Procedimiento
Para comparar fracciones, primero las reduciremos a común denominador y luego las ordenaremos comparando los numeradores.
Ejemplo: Comparación de fracciones
Ordena las siguientes fracciones: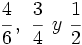 
Calculamos el m.c.m. de los denominadores:
- .
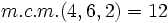A continuación, las reducimos a común denominador:
Ordenamos las fracciones obtenidas, y a partir de ellas las fracciones de partida:
Ejercicios propuestos
 Ejercicios propuestos: Reducción de fracciones a común denominador (Pág. 136)
|
