Relaciones de proporcionalidad entre magnitudes (1º ESO)
De Wikipedia
| Revisión de 15:52 27 sep 2016 Coordinador (Discusión | contribuciones) (→Relación de proporcionalidad directa) ← Ir a diferencia anterior |
Revisión de 15:54 27 sep 2016 Coordinador (Discusión | contribuciones) (→Constante de proporcionalidad) Ir a siguiente diferencia → |
||
| Línea 39: | Línea 39: | ||
| {{p}} | {{p}} | ||
| ===Constante de proporcionalidad=== | ===Constante de proporcionalidad=== | ||
| - | {{Caja_Amarilla|texto=Al valor que resulta de dividir dos magnitudes directamente proporcionales se le llama '''constante de proporcionalidad'''.}} | + | {{Caja_Amarilla|texto=Al dividir dos magnitudes directamente proporcinales siempre se obtiene el mismo valor. A dicho valor se le llama '''constante de proporcionalidad'''.}} |
| {{Ejemplo_simple|titulo=Ejemplo:|contenido= | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| Línea 86: | Línea 86: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ===Constante de proporcionalidad=== | ===Constante de proporcionalidad=== | ||
Revisión de 15:54 27 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 152)
Relación de proporcionalidad directa
Dos magnitudes son directamente proporcionales cuando al multiplicar (resp. dividir) una de ellas por un número, la otra queda multiplicada (resp. dividida) por el mismo número.
La capacidad de un depósito de agua y el tiempo que tarda en llenarse son magnitudes directamente proporcionales, ya que si el depósito tiene el doble (o el triple,...) de capacidad, el tiempo que tarda en llenarse es el doble (o el triple,...).
Capacidad (litros) |
100 |
200 |
300 |
400 |
500 |
Tiempo (min) |
5 |
10 |
15 |
20 |
25 |
Constante de proporcionalidad
Al dividir dos magnitudes directamente proporcinales siempre se obtiene el mismo valor. A dicho valor se le llama constante de proporcionalidad.
En el ejemplo anterior en el que relacionabamos la capacidad de un depósito con el tiempo que tardaba en llenarse
Capacidad (litros) |
100 |
200 |
300 |
400 |
500 |
Tiempo (min) |
5 |
10 |
15 |
20 |
25 |
se observa que:
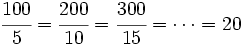
La constante de proporcinalidad es 20.
Constante de proporcionalidad
Relación de proporcionalidad inversa
Ejercicios propuestos
|
Ejercicios propuestos: Relaciones de proporcionalidad entre magnitudes |

