Plantilla:Número de soluciones de un sistema
De Wikipedia
Revisión de 17:57 30 oct 2016
- Un sistema es compatible si tiene solución e incompatible si no la tiene.
- Un sistema es determinado si tiene un número finito de soluciones e indeterminado si tiene infinitas soluciones.
- Usaremos las siguientes siglas para abreviar:
- S.C.D. : Sistema Compatible Determinado (un número finito de soluciones)
- S.C.I. : Sistema Compatible Indeterminado (infinitas soluciones)
- S.I. : Sistema Incompatible (sin solución)
Número de soluciones de un sistema 2x2 de ecuaciones lineales
Un sistema 2x2 de ecuaciones lineales puede ser:
- Compatible determinado (S.C.D.): 1 solución
- Compatible indeterminado (S.C.I.): Infinitas soluciones.
- Incompatible (S.I): 0 soluciones.
En efecto, razonando a partir de sus representaciones gráficas:
- Si las dos rectas se cortan en un punto: 1 solución (S.C.D.)
- Si las dos rectas son coincidentes: Infinitas soluciones (S.C.I.)
- Si las rectas son paralelas: 0 soluciones (S.I.)
En la siguiente actividad veremos un ejemplo de cada uno de los tres casos anteriores.
|
Actividad Interactiva: Soluciones de un sistema
Actividad 1: Sistema incompatible.
Actividad: Dado el siguiente sistema 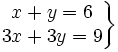 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados:
Actividad 2: Sistema compatible indeterminado.
Actividad: Dado el siguiente sistema 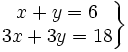 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados:
Actividad 3: Sistema compatible determinado.
Actividad: Dado el siguiente sistema 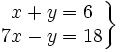 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados: |

