Plantilla:Término general de una progresión geométrica
De Wikipedia
| Revisión de 15:51 14 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:20 25 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 53: | Línea 53: | ||
| *Ejemplos. | *Ejemplos. | ||
| *Término general de una progresión geométrica. | *Término general de una progresión geométrica. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo|titulo=Ejercicio resuelto: ''Progresión geométrica'' | ||
| + | |enunciado={{p}} | ||
| + | En una progresión geométrica de términos positivos, <math>a_1=3\;</math> y <math>a_3 = 6\;</math>. | ||
| + | Halla <math>a_n\;</math>, <math>a_{20}\;</math> y <math>a_{21}\;</math>. | ||
| + | |sol= | ||
| + | <math>a_3=a_1 \cdot r^2 \rightarrow 6 = 3 \cdot r^2 \rightarrow r^2=\cfrac{6}{3}=2 \rightarrow r=\pm \sqrt{2}</math> | ||
| + | |||
| + | Como la progresión es de términos positivos, sólo nos vale el valor posivo: {{sube|porcentaje=20%|contenido=<math>r=\sqrt{2}</math>}}. | ||
| + | {{p}} | ||
| + | <math>a_n= a_1 \cdot r^{n-1} = 3 \cdot (\sqrt{2})^{n-1}</math> | ||
| + | |||
| + | <math>a_{20} = 3 \cdot (\sqrt{2})^{20-1} = 3 \cdot (\sqrt{2})^{19} = 3 \cdot 2^9 \cdot \sqrt{2} =1536 \sqrt{2}</math> | ||
| + | |||
| + | <math>a_{21} = 3 \cdot (\sqrt{2})^{21-1} = 3 \cdot (\sqrt{2})^{20} = 3 \cdot 2^{10} =3072</math> | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=Encuentra el término general de una progresión geométrica dada. | ||
| + | |enlace=[https://ggbm.at/gtqvQpFm Autoevaluación: Término general de una progresión geométrica] | ||
| }} | }} | ||
Revisión de 18:20 25 nov 2016
Término general de una progresión geométrica
El término general, 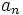 , de una progresión geométrica de razón
, de una progresión geométrica de razón  es:
es:
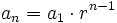
En efecto, de forma intuitiva:
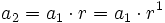

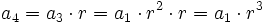
........................
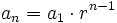
Demostración por el método de inducción completa:
Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural.
Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula:
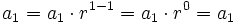
con lo que queda comprobada para n=1.
Supongamos que la fórmula es cierta para el valor n:
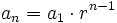 . [1]
. [1]Por ser una progresión geométrica cada término se obtiene multiplicando por r el anterior término:
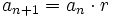 [2]
[2]Debemos comprobar que se cumple para el valor n+1:
![a_{n+1}\begin{matrix} ~_{[2]}~ \\ = \\ ~ \end{matrix}a_n \cdot r \begin{matrix} ~_{[1]}~ \\ = \\ ~ \end{matrix} a_1 \cdot r^{n-1} \cdot r =a_1 \cdot r^{((n+1)-1)}](/wikipedia/images/math/b/5/0/b50e2fb51571873946095ab7579f8b90.png)
- Definición de progresión geométrica.
- Ejemplos.
- Término general de una progresión geométrica.
Ejercicio resuelto: Progresión geométrica
En una progresión geométrica de términos positivos, 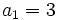 y
y 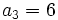 .
Halla
.
Halla  ,
, 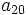 y
y 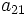 .
.
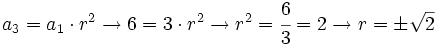
Como la progresión es de términos positivos, sólo nos vale el valor posivo: 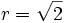 .
.
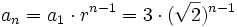
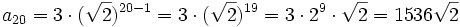
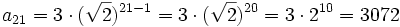
Encuentra el término general de una progresión geométrica dada.

