Plantilla:Dominio e imagen de una función (Bachiller)
De Wikipedia
| Revisión de 18:28 8 dic 2016 Coordinador (Discusión | contribuciones) (→Razones para restringir el dominio de una función) ← Ir a diferencia anterior |
Revisión de 11:42 9 dic 2016 Coordinador (Discusión | contribuciones) (→Cálculo del dominio de una función) Ir a siguiente diferencia → |
||
| Línea 87: | Línea 87: | ||
| |duracion=9'14" | |duracion=9'14" | ||
| |sinopsis=:15 ejemplos. | |sinopsis=:15 ejemplos. | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0134_01.htm | + | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/3501-quince-ejercicios-4#.WEqJ97LhC1s |
| }} | }} | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| Línea 93: | Línea 93: | ||
| |duracion=11'08" | |duracion=11'08" | ||
| |sinopsis=:15 ejemplos. | |sinopsis=:15 ejemplos. | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0134_02.htm | + | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/3502-dieciseis-ejercicios-4#.WEqKQrLhC1s |
| }} | }} | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| Línea 99: | Línea 99: | ||
| |duracion=9'24" | |duracion=9'24" | ||
| |sinopsis=10 ejemplos. | |sinopsis=10 ejemplos. | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0134_03.htm | + | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/3503-diez-ejercicios-4#.WEqKWbLhC1s |
| }} | }} | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
Revisión de 11:42 9 dic 2016
Dominio e imagen de una función
- Al conjunto de los valores que puede tomar la variable independiente
 , se le llama dominio de definición de la función. Lo representaremos por
, se le llama dominio de definición de la función. Lo representaremos por 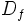 ó
ó 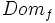
- La imagen, rango o recorrido de una función es el conjunto de valores que puede tomar la variable dependiente
 . Lo representaremos por
. Lo representaremos por 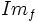 o
o 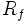 .
.
En esta escena podrás visualizar el dominio y la imagen de una función. Podrás elegir entre un tramo de recta (función lineal) o de parábola (función cuadrática).
El "dominio de definición" de la función "f" se denota Domf, y es el conjunto que forman los números reales "x" que tienen imagen segun "f"; o sea, los "x" tales que al calcular "f(x)" no se viola ninguna Regla Sagrada. A la hora de representar la gráfica de "f" lo primero SIEMPRE es determinar Domf, pues así sabremos en qué puntos del eje de abcisas hay curva y en qué puntos no la hay.
Razones para restringir el dominio de una función
- Imposibilidad de realizar alguna operación con ciertos valores de
 (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos, logaritmos de valores no positivos)
(Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos, logaritmos de valores no positivos)
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos)
- Por voluntad de quien propone la función.
Ejemplo: Dominio de definición de una función
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
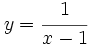
- b)
- c)
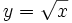
- c)
- d)
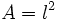 (Área de un cuadrado de lado
(Área de un cuadrado de lado 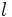 )
)
- d)
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png) , por voluntad del que ha definido la función, ya que, en principio, cualquier valor de
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
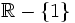 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
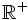 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
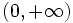 , porque el lado de un cuadrado sólo puede tomar valores positivos
, porque el lado de un cuadrado sólo puede tomar valores positivos
Cálculo del dominio de una función
Hay ciertas reglas en matemáticas que no se pueden violar. Estas reglas afectan a la hora de determinar el dominio de una función. Aquí las vamos a recordar:
- Prohibido dividir por cero.
- Toda raíz de índice par de un número negativo no es un número real.
- El logaritmo (en cualquier base) de un número no positivo no es un número real.
AVISO: será inmisericordemente suspendido ipso facto todo el que viole una Regla Sagrada; caerán sobre él toneladas de desprestigio y deshonor, y el estigma de tan ignominioso acto apestará la honra de su linaje por los siglos de los siglos.
Hay funciones que a la hora de trabajar con ellas no presentan ningún problema; otras sin embargo son realmente peligrosas.
En relación a los tres conceptos fundamentales del Cálculo (límite, continuidad y derivada de una función "f" en un punto "c"), y debido a las posibles violaciones de las tres Reglas Sagradas, las funciones son como las serpientes: las hay inofensivas y las hay peligrosas. Por eso, al trabajar con una función "f" en el punto "c", lo primero es invertir un par de segundos en analizar si "f" es o no peligrosa en "c". Naturalmente, si es peligrosa, pondremos todos nuestros sentidos en estado de máxima concentración y alerta, para así intentar evitar que nos mande al otro barrio.
En este vídeo vemos ejemplos en los que analizamos la peligrosidad de trabajar (límite, continuidad, derivada) con una cierta función "f" en un cierto punto "c".
Todo se reduce a analizar si en "c" se viola alguna Regla Sagrada; a saber:
- Prohibido dividir por cero.
- Toda raíz de índice par de un número negativo no es un número real.
- El logaritmo (en cualquier base) de un número no positivo no es un número real.
Ejemplos: Dominio de definición de una función
- 15 ejemplos.
- 15 ejemplos.
10 ejemplos.
- 11 ejemplos.
- 7 ejemplos.
- 8 ejemplos.
- 4 ejemplos.
- 6 ejemplos.
- 7 ejemplos.
7 ejemplos.

