Familias de funciones elementales (1ºBach)
De Wikipedia
| Revisión de 17:27 11 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:29 11 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 58: | Línea 58: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades=== | ||
| {{Teorema_sin_demo|titulo=Propiedades de la función lineal|enunciado=Las funciones lineales <math>y=mx+n\;</math> cumplen las siguientes propiedades: | {{Teorema_sin_demo|titulo=Propiedades de la función lineal|enunciado=Las funciones lineales <math>y=mx+n\;</math> cumplen las siguientes propiedades: | ||
| Línea 93: | Línea 92: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades=== | + | |
| - | {{Teorema_sin_demo|titulo=Propiedades de la función lineal|enunciado=Las funciones lineales <math>y=ax^2+bx+c\;</math> cumplen las siguientes propiedades: | + | {{Teorema_sin_demo|titulo=Propiedades de la función cuadrática|enunciado=Las funciones lineales <math>y=ax^2+bx+c\;</math> cumplen las siguientes propiedades: |
| *Son continuas en su dominio, que es <math>D_f=\mathbb{R}</math>. | *Son continuas en su dominio, que es <math>D_f=\mathbb{R}</math>. | ||
| Línea 124: | Línea 123: | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades=== | ||
| {{Teorema_sin_demo|titulo=Propiedades de la función irracional|enunciado=Las funciones del tipo <math>y=\sqrt[n]{x}</math> cumplen las siguientes propiedades: | {{Teorema_sin_demo|titulo=Propiedades de la función irracional|enunciado=Las funciones del tipo <math>y=\sqrt[n]{x}</math> cumplen las siguientes propiedades: | ||
| Línea 134: | Línea 132: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | |||
| ==Funciones de proporcionalidad inversa== | ==Funciones de proporcionalidad inversa== | ||
| {{Tabla75|celda2=[[Imagen:prop_inversa.png|center|thumb|230px|Funciones de proporcionalidad inversa]] | {{Tabla75|celda2=[[Imagen:prop_inversa.png|center|thumb|230px|Funciones de proporcionalidad inversa]] | ||
| Línea 163: | Línea 160: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema_sin_demo|titulo=Propiedades|enunciado= | + | {{Teorema_sin_demo|titulo=Propiedades de la función de proporcionalidad inversa|enunciado= |
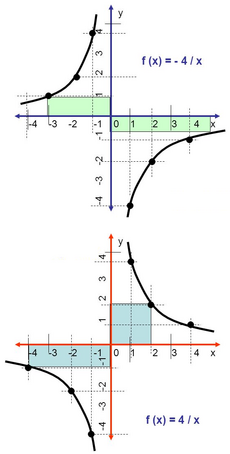
| Las funciones de proporcionalidad inversa <math>y=\cfrac{k}{x}\;</math> cumplen las siguientes propiedades: | Las funciones de proporcionalidad inversa <math>y=\cfrac{k}{x}\;</math> cumplen las siguientes propiedades: | ||
| Línea 205: | Línea 202: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | |||
| ==Funciones exponenciales== | ==Funciones exponenciales== | ||
| {{funcion exponencial de base a}} | {{funcion exponencial de base a}} | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades=== | ||
| {{Propiedades de la funcion exponencial}} | {{Propiedades de la funcion exponencial}} | ||
| {{p}} | {{p}} | ||
| Línea 215: | Línea 210: | ||
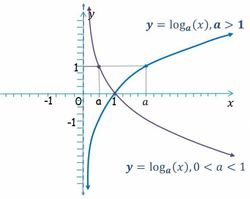
| {{Función logarítmica de base a}} | {{Función logarítmica de base a}} | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades=== | ||
| {{Propiedades de la funcion logaritmica}} | {{Propiedades de la funcion logaritmica}} | ||
| {{p}} | {{p}} | ||
Revisión de 17:29 11 dic 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 250)
Funciones algebraicas y trascendentes
- Las funciones algebraicas son aquellas en las que las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
- Las funciones trascendentes son aquellas que no son algebraicas.
La función "f" se dice "algebraica" si las operaciones que deben realizarse para determinar el número real "f(x)" son las llamadas algebraicas: suma, resta, multiplicación, división, potenciación de exponente constante y radicación de ínidice constante. Si "f" no es algebraica, se dice "trascendente".
Funciones lineales
Sean 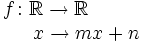
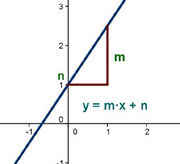
Representación de la familia de funciones lineales. |
Propiedades de la función lineal
Las funciones lineales 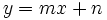 cumplen las siguientes propiedades:
cumplen las siguientes propiedades:
- Son continuas en su dominio, que es
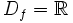 .
.
- Su gráfica es una recta que cortan al eje Y en
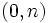 .
.
- Si
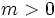 son crecientes, si
son crecientes, si  son decrecientes y si
son decrecientes y si 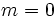 son constantes.
son constantes.
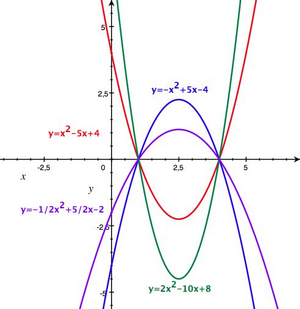
Funciones cuadráticas
Sean 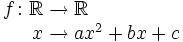 Representación de la familia de funciones cuadráticas. Propiedades de la función cuadrática Las funciones lineales
|
Funciones irracionales
Sea ![y=\sqrt[n]{x}](/wikipedia/images/math/c/7/b/c7b0045f1674ed5dee699a4a9d3eefef.png) Representación de la familia de funciones irracionales. |
Funciones de proporcionalidad inversa
Sea 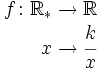 El numero Este tipo de funciones se llaman así porque si Representación de la familia de funciones de proporcionalidad inversa. Propiedades de la función de proporcionalidad inversa Las funciones de proporcionalidad inversa
|
Una función homográfica es una función racional del tipo:
|
|
Proposición
Si transformamos una función de proporcionalidad inversa por medio de traslaciones horizontales y verticales, el resultado es una función homográfica.
Si partimos de una función de proporcionalidad inversa:
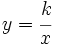
y sobre ella efectuamos traslaciones verticales y horizontales, nos quedaría:
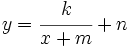
Desarrollando esta expresión:
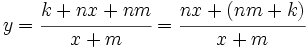
Representación de la familia de funciones homográficas.
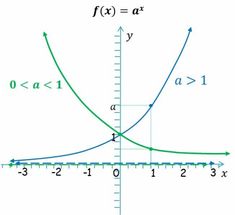
Funciones exponenciales
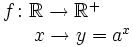
|
Propiedades de la función exponencial Las funciones exponenciales de base
|
Funciones logarítmicas
Sea 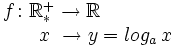
|
Propiedades de la función logarítmica Las funciones exponenciales de base
|
Funciones trigonométricas
Ver tema: Funciones trigonométricas o circulares
Ejercicios propuestos
|
Ejercicios propuestos: Concepto de función y de dominio de una función |
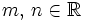 . Se define la función lineal como:
. Se define la función lineal como:
 recibe el nombre de pendiente.
recibe el nombre de pendiente.
 recibe el nombre de ordenada en el origen.
recibe el nombre de ordenada en el origen.
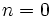 se llama función de proporcionalidad directa.
se llama función de proporcionalidad directa.
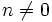 se llama función afín.
se llama función afín.
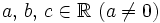 . Se define la función cuadrática como:
. Se define la función cuadrática como:
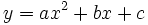 cumplen las siguientes propiedades:
cumplen las siguientes propiedades:
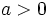 y hacia bajo si
y hacia bajo si 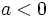 .
.
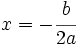 que pasa por el vértice de la parábola.
que pasa por el vértice de la parábola.
 . Se define la función raíz de índice n como:
. Se define la función raíz de índice n como:
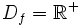 si
si 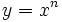
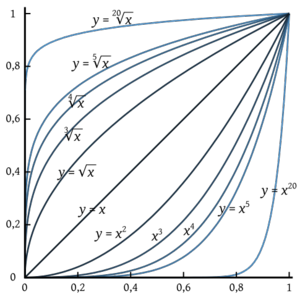
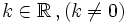 . Las función de proporcionalidad inversa se define como
. Las función de proporcionalidad inversa se define como
 recibe el nombre de constante de proporcionalidad inversa.
recibe el nombre de constante de proporcionalidad inversa.
 e
e  son cantidades correspondientes de dos magnitudes inversamente proporcionales, con constante de proporcionalidad
son cantidades correspondientes de dos magnitudes inversamente proporcionales, con constante de proporcionalidad 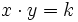 .
.
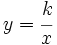 cumplen las siguientes propiedades:
cumplen las siguientes propiedades:
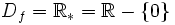 .
.
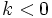 y decrecientes si
y decrecientes si 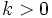 .
.
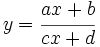
 . Se define la función exponencial de base
. Se define la función exponencial de base  como:
como:
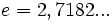 (número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
(número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
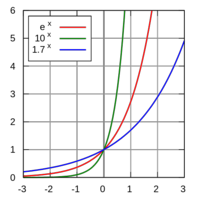
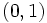 y
y 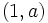 .
.
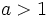 son crecientes
son crecientes
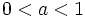 son decrecientes.
son decrecientes.
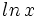 .
.
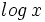 (sin especificar la base).
(sin especificar la base).
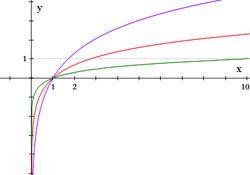
 .
.
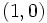 y
y 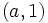 .
.
![\sqrt[n]{x}](/wikipedia/images/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) .
.
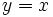 .
.