Plantilla:Triángulos semejantes
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:26 21 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:58 24 abr 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | |||
| Se dice que dos figuras geométricas, y en particular dos [[triángulos]], son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes. | Se dice que dos figuras geométricas, y en particular dos [[triángulos]], son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes. | ||
| {{p}} | {{p}} | ||
| Línea 23: | Línea 22: | ||
| (*) Dos elementos de dos figuras son '''homólogos''' si ocupan el mismo lugar en ambas figuras. | (*) Dos elementos de dos figuras son '''homólogos''' si ocupan el mismo lugar en ambas figuras. | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Ejemplo: Triángulos semejantes | ||
| + | |duracion=5'09" | ||
| + | |sinopsis=Resolución de problemas mediante sistemas de ecuaciones lineales | ||
| + | |url1=http://www.unicoos.com/clase/matematicas/2-eso/semejanza-y-teorema-de-thales/semejanza/semejanza-de-triangulos-01 | ||
| + | }} | ||
| + | {{p}} | ||
Revisión de 10:58 24 abr 2017
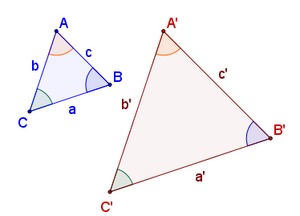
Se dice que dos figuras geométricas, y en particular dos triángulos, son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes.
Matemáticamente, la semejanza de triángulos la podemos expresar de la siguiente manera:
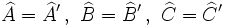
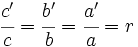
|
(*) Dos elementos de dos figuras son homólogos si ocupan el mismo lugar en ambas figuras.
Resolución de problemas mediante sistemas de ecuaciones lineales
 se le llama razón de semejanza.
se le llama razón de semejanza.